(х-3у)(х+3у)=х²-9у²
Объяснение:
формула разности квадратов
(а-б)(а+б)=а²-б².
См. объяснение и графики (в прикреплении)
Объяснение:
Чтобы найти координаты точки пересечения графиков двух функций, необходимо: 1) приравнять их; 2) из этого равенства найти х; 3) по найденному значению х найти у.
Задание В
1) приравняем х = 3х-4;
2) 2х = 4, х = 2;
3) если в первое уравнение подставить х = 2, то получим у = 2.
ответ: координаты точки пересечения х = 2, у = 2.
Построение графика.
1) Графики строим по точкам.
2) Для каждого графика необходимо 2 точки, т.к. это прямые линии.
3) Точки для графика у=х:
1) х = 0, у = 0; 2) х = 5; у = 5.
4) Точки для графика у=3х-4:
1) х = 0, у = - 4; 2) х = 3; у = 5.
ВНИМАНИЕ: оба графика должны пройти через точку пересечения.
Задание Г
) приравняем 3х + 2 = -0,5 х - 5;
2) 3,5 х = - 7, х = - 2;
3) если в первое уравнение подставить х = - 2, то получим у = -4.
ответ: координаты точки пересечения х = - 2, у = - 4.
Построение графика.
1) Графики строим по точкам.
2) Для каждого графика необходимо 2 точки, т.к. это прямые линии.
3) Точки для графика у=3х+2:
1) х = 0, у = 2; 2) х = 2; у = 8.
4) Точки для графика у=-0,5х-5:
1) х = 0, у = - 5; 2) х = 4; у = - 7.
Примечание: оба графика должны пройти через точку их пересечения.
а)
Множество четных натуральных чисел: 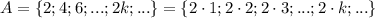
Множество нечетных натуральных чисел: 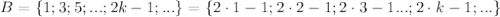
Можно заметить, что если от любого элемента множества А отнять 1, то получится элемент множества B.
Тогда, если x - четное натуральное число, y - нечетное натуральное число, то:
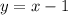
б)
Множество квадратов натуральных чисел: 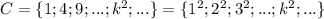
Множество кубов натуральных чисел: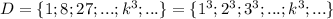
Можно заметить, что если из любого элемента множества C извлечь квадратный корень и получившееся число возвести в куб, то получится элемент множества D.
Тогда, если x - квадрат натурального числа, y - куб натурального числа, то:
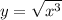
Объяснение:
(x – 3y) (x + 3y)=x²-9y²
OTBET:c