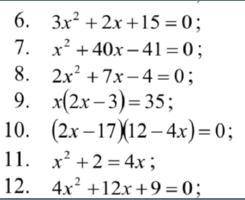
3х²+2х+15=0; D=b²-4ac=4-60<0 решений нет
х²+40х-41=0; по теореме Виета х=-41; х=1.
2х²+7х-4=0; D=b²-4ac=49+32=81; х=(-7±√81)/4=(-7±9)/4; х=0,5; х=-4
х(2х-3)=35; 2х²-3х-35=0; D=b²-4ac=9+280=289; √289=±17; х=(3±17)/4; х=5; х=-3,5
(2х-17)(12-4х)=0; 2х-17=0; 2х=17; х=8,5; 12-4х=0; 4х=12; х=3
х²-4х+2=0; D<0; решений нет
4х²+12х+9=0; D=b²-4ac=144-144=0; х=-12/8=-1,5.
Объяснение:
1). (x+3)(2-x)/x+6≥0 Умножим обе стороны неравенства на x+6 и получим (x+3)(2-x)≥0. Отсюда (x+3)≥0 и (2-x)≥0. Тогда x≥-3 и x≤2
2). 2х²+7х+5>0 Приравняем данное неравенство к равенству.
2х²+7х+5 = 0
D=-7²-4·2·5 = 49-40 = √9 = 3²
x1= (-7+3)/2·2 = -4/4 = -1
x2= (-7-3)/4 = - 2,5
3). (x-2)²(x²+6x-9)<0
(x-2)²<0 и (x²+6x-9)<0
Решим сначала (x-2)²<0
= x²-2·2·x+2²<0 = x²-4x+4<0 Приравняем данное неравенство к нолю и получим x²-4x+4=0
D=-4+²-4·1·4=16-16+ = √0 = 0
x1 = (4+0)/2·1= 4/2 = 2
x2 = (4-0)/2·1= 4/2 = 2
Теперь решим (x²+6x-9)<0. Приравняем данное неравенство к нолю и получим x²+6x-9=0
D= 6²-4·1·(-9) = 36+36 = √72
x1 = (-6+√72)/2 = -3+(√72/2)
x2 = (-6-√72)/2 = -3-(√72/2)
4). x²-5x+4/x³-64>0 Умножим обе стороны неравенства на x³-64 и получим: x²-5x+4>0. Приравняем данное неравенство к нолю.
x²-5x+4=0
D=-5²-4·1·4 = 25-16 = √9 = 3²
x1= (5+3)0/2= 8/2= 4
x2= (5-3)/2 = 2/2 = 1
5). (x-2)(2+x)(5-x)≤0 Отсюда (x-2)≤0 (2+x)≤0 (5-x)≤0
Тогда: x≤2, x≤-2 и x≥5
1)2((8+x)+x)=20
8+2x=20:2
8+2х=10
2х=10-8
2х=2
х=2:2
х=1-ширина
8+х=8+1=9 - длина
2)2х+х=441
3х=441
х=441:3
х=147-второе число
3х=294-первое число
3)х+у+х-у=140+14
2х=154
х=154:2
х=77-первое число
77+у=140
у=140-77
у=63-второе число
4) х+(х+1)+(х+2)=201
3х+3=201
3х=201-3
3х=198
х= 198:3
х=66
х+1=67
х+2=68
Это числа 66,67 и 68
У фото все есть что и как делать