Алгебра: 11 черта дроби х+5= -11 черта дроби 5

11 черта дроби х+5= -11 черта дроби 5

👇

Увидеть ответ

Ответ:

tihon123123

06.04.2023

В ответе получается 0,если я тебя правильно поняла

4,7(31 оценок)

Открыть все ответы

Ответ:

alinurkanat

06.04.2023

ответ:Які вони, сучасні Журдени?

Твори, що ввійшли до скарбниці світової класики можна розділити на два види: епохальні і вічні. Епохальні твори відображають тенденції притаманні певному конкретному періоду, а вічні – це ті, що не втрачають своєї актуальності ніколи. Саме до категорії вічних творів належить іронічна комедія Мольєра „Міщанин-шляхтич”. Автор піднімає складну і суперечливу проблему сліпого бажання людини здаватися більш значною ніж вона є насправді. Це явище характерне і для нашого часу, адже так часто сучасні люди вдягають чужі маски, які їм зовсім не пасують і стараються грати роль, яка їм не по зубах.

Головний герой п’єси пан Журден , є одним з найбільш кумедних персонажів світової літератури. Над ним потішаються, як і дійові персонажі, так і читачі. А справді, що може виглядати більш комічно ніж підстаркуватий торговець, що несподівано захотів стати аристократом. Це бажання є настільки сильним, що Журден, всупереч своїм обмеженим здібностям, старається робити речі, які йому геть не виходять: він вчиться співати, хоча зовсім не має музичних даних, вивчає кілька танців, які вдаються йому жалюгідно, махає шпагою, хоча від природи він неповороткий. Всі навколо гають за цією комедією і підіграють Журдену, вони кажуть йому те, що він хоче почути, заради власної вигоди вдаються до грубих лестощів. Проте головний герой не хоче помічати цієї брехні, він всіма силами старається дотримуватися стандартів дворянства, живе в світі власних ілюзій, де бачить себе великим вельможею.

Зараз більше немає ні дворянських титулів, ні аристократії, але люди й далі прагнуть вдягнути на себе маску, сховати під нею своє справжнє обличчя, приховати свою сутність. У всі часи були ті, кого не задовольняло їхнє життя, соціальний статус чи матеріальний стан. З такої ситуації є два виходи ший і складніший ший варіант і вибрав для себе пан Журден. А полягає цей вихід у тому, що людина, незадоволена зовнішнім світом, будує свій власний вигаданий світ ілюзій. Вона живе в ньому, свої мрії сприймає як реальність, дивиться на оточуючих через призму власної вигадки. Але рано чи пізно, цей так званий „замок з піску” руйнується і людина опиняється з одним лише розчаруванням. Особа, котра обрала для себе складніший варіант, мусить тяжко працювати для досягнення своєї цілі, але в результаті її праця приносить бажані плоди, бо немає нічого неможливого головне вірити в себе і не боятися наяву, а не в уяві міняти свою долю. Це підтверджують слова видатного політичного діяча Великобританії Вінстона Черчилля: „Коли ти кажеш, що щось можеш або чогось не можеш, ти завжди маєш рацію.”

П’єса Мольєра „Міщанин-шляхтич” – це історія життя слабкої особистості, яка дозволяла іншим себе обманювати і сама собі брехала. Головний герой п’єси, пан Журден, не хоче ні чути, ні бачити правди, бо істинна далеко не така солодка, як мед лестощів. А змінити щось в реальному житті набагато складніше ніж втекти у власний примарний світ ілюзій та мрій.

Объяснение:

4,4(69 оценок)

Ответ:

xomahgf

06.04.2023

ответ: $\left[-5;-\dfrac{7+2\sqrt{7}}{3}\right)\cup\left(-\dfrac{7+2\sqrt{7}}{3};-\dfrac{7}{2}\right)\cup\left(-1;-\dfrac{1}{2}\right]\cup\left\{\dfrac{-11+4\sqrt{7}}{9};\dfrac{7-2\sqrt{7}}{3};\dfrac{7+2\sqrt{7}}{3}\right\}$ Объяснение:

Исходная дробь равносильна следующей системе (числитель равен нулю, знаменатель не равен нулю + ОДЗ):

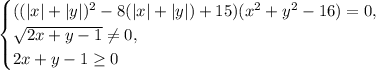
$\begin{cases}((|x|+|y|)^2-8(|x|+|y|)+15)(x^2+y^2-16)=0,\\ \sqrt{2x+y-1}\neq 0,\\ 2x+y-1\geq 0 \end{cases}$

В первом уравнении произведение равно нулю, когда хотя бы один из множителей равен нулю. Второе неравенство равносильно тому, что подкоренное выражение не равно нулю. Значит, вместе второе и третье образуют неравенство 2x + y - 1 > 0 ⇔ y > -2x + 1. Вернёмся к первому уравнению:

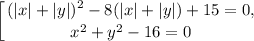
$\displaystyle\left [ {{(|x|+|y|)^2-8(|x|+|y|)+15=0,} \atop {x^2+y^2-16=0}} \right.$

В первом уравнении сделаем замену |x| + |y| = t.

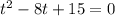
t^2-8t+15=0

По теореме Виета 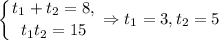$\displaystyle\left \{ {{t_1+t_2=8,} \atop {t_1t_2=15}} \right. \Rightarrow t_1=3,t_2=5$

Получаем 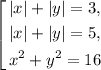$\left[\begin{gathered}|x|+|y|=3,\\|x|+|y|=5,\\ x^2+y^2=16\end{gathered}\right.$

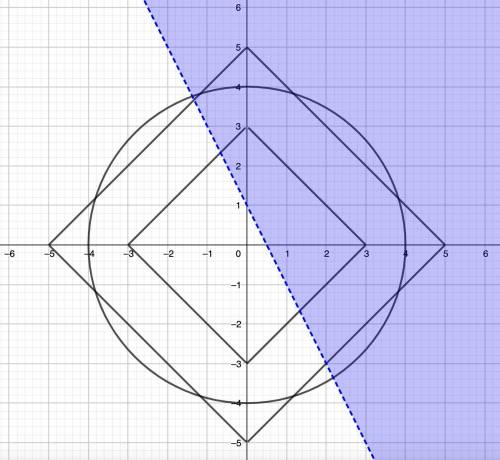
Третье уравнение — уравнение окружности с центром (0; 0) и радиусом 4. Первые два уравнения — уравнения квадратов с центром в точке (0; 0), наклонённых на 45° и диагоналями 6 и 10: действительно, если раскрыть модуль y, а всё без y перенести в правую сторону, то при y ≥ 0 y = -|x| + 3, при y < 0 y = |x| - 3. Аналогично с |x| + |y| = 5.

Учтём ограничение y > -2x + 1: нам подохдят все y, что выше прямой -2x + 1. Всё вместе это выглядит, как на первой картинке. Теперь нужно обрезать всё, что не попадает в синюю область (см. вторую картинку).

Для выполнения второго задания вычислим точки пересечения квадратов и окружности с прямой y = -2x + 1, а также точки пересечения окружности и большого квадрата.

|x|+|1-2x|=3

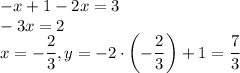
При x < 0: $-x+1-2x=3\\-3x=2\\x=-\dfrac{2}{3}, y=-2\cdot\left(-\dfrac{2}{3}\right)+1=\dfrac{7}{3}$

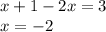При 0 ≤ x < 0,5: $x+1-2x=3\\x=-2$ — не подходит

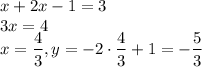
При x ≥ 0,5: $x+2x-1=3\\3x=4\\x=\dfrac{4}{3},y=-2\cdot \dfrac{4}{3}+1=-\dfrac{5}{3}$

|x|+|1-2x|=5

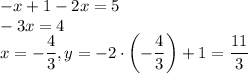
При x < 0: $-x+1-2x=5\\-3x=4\\x=-\dfrac{4}{3}, y=-2\cdot\left(-\dfrac{4}{3}\right)+1=\dfrac{11}{3}$

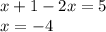При 0 ≤ x < 0,5: $x+1-2x=5\\x=-4$ — не подходит

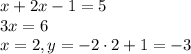
При x ≥ 0,5: $x+2x-1=5\\3x=6\\x=2,y=-2\cdot 2+1=-3$

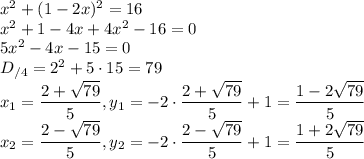
$x^2+(1-2x)^2=16\\x^2+1-4x+4x^2-16=0\\5x^2-4x-15=0\\D_{/4}=2^2+5\cdot 15=79\\x_1=\dfrac{2+\sqrt{79}}{5},y_1=-2\cdot\dfrac{2+\sqrt{79}}{5}+1=\dfrac{1-2\sqrt{79}}{5}\\x_2=\dfrac{2-\sqrt{79}}{5},y_2=-2\cdot\dfrac{2-\sqrt{79}}{5}+1=\dfrac{1+2\sqrt{79}}{5}$

$\displaystyle\left \{ {{|x|+|y|=5,} \atop {x^2+y^2=16}} \right.\left \{ {{|x|+\sqrt{16-x^2}=5,} \atop {|y|=\sqrt{16-x^2}}} \right.$

Решим первое уравнение:

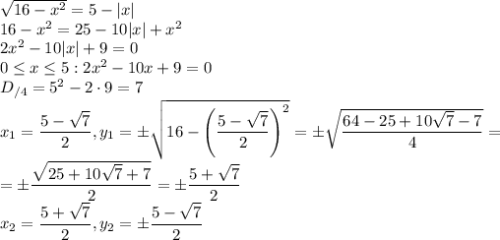
$\sqrt{16-x^2}=5-|x|\\16-x^2=25-10|x|+x^2\\2x^2-10|x|+9=0\\0\leq x\leq 5: 2x^2-10x+9=0\\D_{/4}=5^2-2\cdot 9=7\\x_1=\dfrac{5-\sqrt{7}}{2},y_1=\pm\sqrt{16-\left(\dfrac{5-\sqrt{7}}{2}\right)^2}=\pm\sqrt{\dfrac{64-25+10\sqrt{7}-7}{4}}=\\=\pm\dfrac{\sqrt{25+10\sqrt{7}+7}}{2}=\pm\dfrac{5+\sqrt{7}}{2}\\x_2=\dfrac{5+\sqrt{7}}{2},y_2=\pm\dfrac{5-\sqrt{7}}{2}$

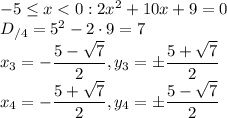
$-5\leq x$

Прямая y = px - 1 — прямая, проходящая через точку (0; -1). Действительно, если подставить x = 0, вне зависимости от параметра p при данном x y = -1. p регулирует наклон прямой. Будем вращать прямую около точки (0; -1) и отмечать промежутки (красным), где прямая "начинает" и "заканчивает" иметь две общие точки (см. третью картинку).

На рисунке отмечены все промежутки и частные случаи, когда прямая имеет две общие точки. Выразим p через x и y:

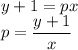
$y+1=px\\p=\dfrac{y+1}{x}$

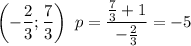
Для $\left(-\dfrac{2}{3};\dfrac{7}{3}\right)\ p=\dfrac{\frac{7}{3}+1}{-\frac{2}{3}}=-5$

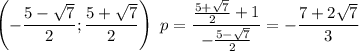
Для $\left(-\dfrac{5-\sqrt{7}}{2};\dfrac{5+\sqrt{7}}{2}\right)\ p=\dfrac{\frac{5+\sqrt{7}}{2}+1}{-\frac{5-\sqrt{7}}{2}}=-\dfrac{7+2\sqrt{7}}{3}$

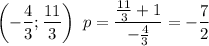
Для $\left(-\dfrac{4}{3};\dfrac{11}{3}\right)\ p=\dfrac{\frac{11}{3}+1}{-\frac{4}{3}}=-\dfrac{7}{2}$

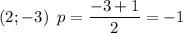
Для $\left(2;-3\right)\ p=\dfrac{-3+1}{2}=-1$

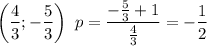
Для $\left(\dfrac{4}{3};-\dfrac{5}{3}\right)\ p=\dfrac{-\frac{5}{3}+1}{\frac{4}{3}}=-\dfrac{1}{2}$

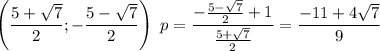
Для $\left(\dfrac{5+\sqrt{7}}{2};-\dfrac{5-\sqrt{7}}{2}\right)\ p=\dfrac{-\frac{5-\sqrt{7}}{2}+1}{\frac{5+\sqrt{7}}{2}}=\dfrac{-11+4\sqrt{7}}{9}$

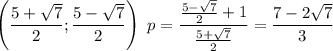
Для $\left(\dfrac{5+\sqrt{7}}{2};\dfrac{5-\sqrt{7}}{2}\right)\ p=\dfrac{\frac{5-\sqrt{7}}{2}+1}{\frac{5+\sqrt{7}}{2}}=\dfrac{7-2\sqrt{7}}{3}$

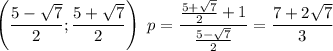
Для $\left(\dfrac{5-\sqrt{7}}{2};\dfrac{5+\sqrt{7}}{2}\right)\ p=\dfrac{\frac{5+\sqrt{7}}{2}+1}{\frac{5-\sqrt{7}}{2}}=\dfrac{7+2\sqrt{7}}{3}$

Итого

$p\in\left[-5;-\dfrac{7+2\sqrt{7}}{3}\right)\cup\left(-\dfrac{7+2\sqrt{7}}{3};-\dfrac{7}{2}\right)\cup\left(-1;-\dfrac{1}{2}\right]\cup\\\cup\left\{\dfrac{-11+4\sqrt{7}}{9};\dfrac{7-2\sqrt{7}}{3};\dfrac{7+2\sqrt{7}}{3}\right\}$