N2
а) 3x+12>0 3x>-12 x>-4
2x-3<0 2x<3 x<1,5 x∈(-4;1,5)
б) 3x+2>2x-3 x>-5
x-5>0 x>5 x∈(5;+∞)
N3
a)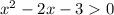 
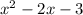=0
x1+x2=2 x1=3
x1
x2=-3 x2=-1
(x-3)(x+1)>0
+ +
_____._______._____
-1 - 3
x∈(-∞;-1)∪(3;+∞).
б)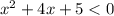 
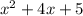=0
d=(4)²-415=16-20=-4
нет решений
в)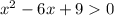 
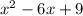=0
(x-3)²=0
(x-3)(x-3)>0
+
_____._____
3 - x∈(-∞;3)
2 sin x – cos x =1
2sin x/2 * cos x/2 – cos² x/2 +sin² x/2 = sin² x/2 + cos² x/2
2sin x/2 * cos x/2 – 2cos² x/2 = 0
2cos x/2 * (sin x/2 – cos x/2) =0
cos x/2 * (sin x/2 – cos x/2) =0
cos x/2 = 0 или sin x/2 – cos x/2 = 0
cos x/2 = 0;
x/2 = π/2 + πk;
x = π + 2πk; k Є Z;
sin x/2 – cos x/2 = 0 – однородное уравнение первой степени.
Делим обе его части на cos x/2 (cos x/2≠ 0, так как,
если cos x/2 = 0, sin x/2 – 0 = 0 => sin x/2 = 0, что противоречит тождеству sin² x/2 + cos² x/2 = 1).
Получим tg x/2 – 1 = 0;
tg x/2 = 1;
x/2 = π/4 + πn;
x = π/2 + 2πn; n Є Z.
1) x = π + 2πk; k Є Z;
y = π/2 + π + 2πk; k Є Z;
y = π + 2πk; k Є Z;
(π + 2πk; k Є Z; π + 2πk; k Є Z;)
2) x = π/2 + 2πn; n Є Z.
y = π/2 + π/2 + 2πn; n Є Z.
y = π + 2πn; n Є Z.
(π + 2πk; k Є Z; π + 2πk; k Є Z)
ответ: (π + 2πk; k Є Z; π + 2πk; k Є Z) ;
(π + 2πk; k Є Z; π + 2πk; k Є Z)
