
Сначала сосчитаем примеры:
1/3 + 0,6 = 1/3 + 6/10= 10/30 + 18/30 = 28/30
1/4+ 0,55 = 1/4 +55/100 = 25/100 +55/100 = 80/100=8/10
1/3 + 0,6 = 1/3+55/100 = 100/300+165/300=265/300=53/60
1/4+0,6 = 1/4+6/10=5/20+12/20=17/20
Теперь приводим дроби к общ. знаменателю:
28/30=56/60
8/10=48/60
53/60
17/20=51/60
Итак, теперь мы получаем что самая большая - 56/60(1/3+0,6)
потом - 53/60(1/3+0,55)
потом - 51/60(1/4+0,6)
ну и самая маленькая - 48/60(1/4+0,55)
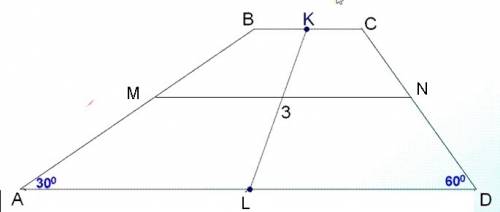
Дано:
ABCD - трапеция
MN - средняя линия
MN=5
BC=KC; AL=LD;
KL=3
∠A=30°; ∠D=60°
Найти CB; AD
1) ∠A +∠D=30°+60°=90°
Сумма углов при основании AD равна 90°
2) Пусть CB=x; AD=y, тогда используем 2 свойства трапеции:
3) Первое свойство
Средняя линия трапеции равна полусумме ее оснований, т.е.
(х+у)/2=MN; => х+у=2·MN => х+у=2·5 =>
х+у=10
4) Второе свойство
Если сумма углов при любом основании равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности, т.е.
(y-х)/2=KL; => у-x=2·KL => y-х=2·3 =>
y-х=6
5) Решаем систему:
х+у=10
у-х=6
Сложим эти уравнения:
х+у+у-х=6+10
2у=16
у=16:2
у=8 см - длина нижнего основания
х=10-8
у=2 см - длина верхнего основания
ответ: 2 см; 8 см
а) (5x + 1) / (x - 2) = (5x + 2) / (x - 3)
ОДЗ:
1) x - 2 ≠ 0
x ≠ 0 + 2
x ≠ 2
2) x - 3 ≠ 0
x ≠ 0 + 3
x ≠ 3
По основному свойству пропорции:
(5x + 1) (x - 3) = (5x + 2) (x - 2)
5x² + 5x · (-3) + x - 3 = 5x² + 5x · (-2) + 2x + 2 · (-2)
5x² - 15x + x - 3 = 5x² - 10x + 2x - 4
- 15x + x - 3 = - 10x + 2x - 4
- 14x - 3 = - 8x - 4
- 14x + 8x = - 4 + 3
- 6x = - 1
x = 1/6 -- соответствует ОДЗ
ответ: x = 1/6.
б) (x - 2) / (x + 13) - (1 - x) / (x - 5) = 0
ОДЗ:
1) x + 13 ≠ 0
x ≠ 0 - 13
x ≠ - 13
2) x - 5 ≠ 0
x ≠ 0 + 5
x ≠ 5
( (x - 5) (x - 2) - (x + 13) (1 - x) ) / ( (x + 13) (x - 5) ) = 0
Умножим обе части уравнения на (x + 13) (x - 5):
(x - 5) (x - 2) - (x + 13) (1 - x) = 0
x² - 2x - 5x + 10 - (x - x² + 13 - 13x) = 0
x² - 2x - 5x + 10 - (- 12x - x² + 13) = 0
x² - 2x - 5x + 10 + 12x + x² - 13 = 0
2x² + 5x - 3 = 0
D = b² - 4ac = 5² - 4 · 2 · (-3) = 25 + 24 = 49
x₁,₂ = (-b ± √D) / 2a = (-5 ± √49) / (2 · 2) = (-5 ± 7) / 4
x₁ = (-5 - 7) / 4 = - 12 / 4 = - 3
x₂ = (-5 + 7) / 4 = 2 / 4 = 1 / 2 = 0,5
ответ: x₁ = - 3; x₂ = 0,5.