
1)3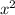 =0
=0
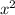 =0
=0
х=0
2)5х-2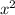 =0
=0
х(5-2х)=0
х=0 5-2х=0
-2х=-5
х=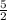
3)2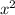 =9х
=9х
2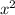 -9х=0
-9х=0
х(2х-9)=0
х=0 2х-9=0
2х=9
х=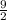
4)48-3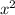 =0 делим на 3
=0 делим на 3
16-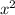 =0
=0
-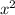 =-16
=-16
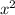 =16
=16
х1=-4 х2=4
5)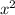 -5=0
-5=0
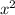 =5
=5
х1=-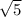 х2=
х2=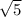
6)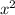 +7=0
+7=0
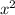 =-7
=-7
НЕТ РЕШЕНИЯ
7)х(6-х)=0
х=0 6-х=0
-х=-6
х=6
8)(х-6)(х+3)=0
х-6=0 х+3=0
х=6 х=-3
9)3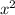 -х-2=0
-х-2=0
Д=1-4*3*(-2)=1+24=25
х1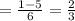
х2
ответ х1=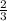 х2=1
х2=1
ОСТАЛЬНО НА ФОТО
Объяснение:
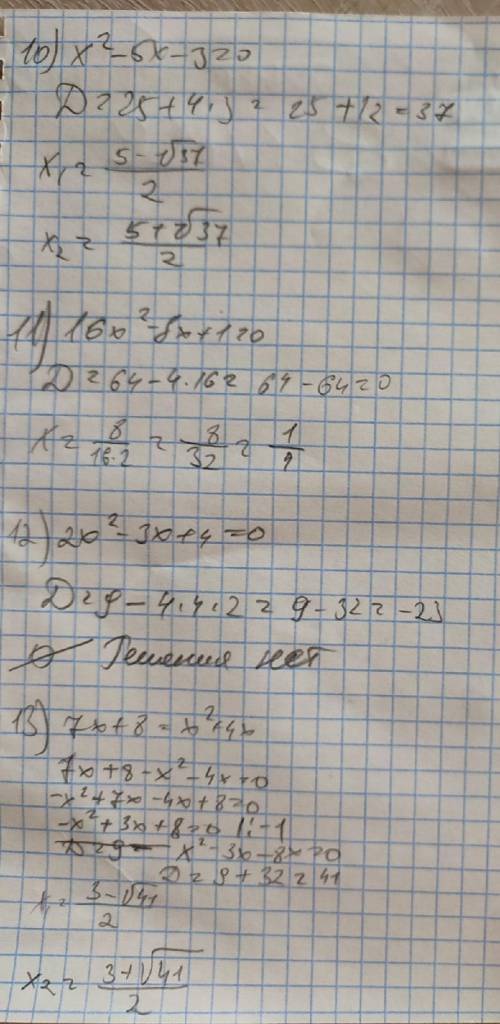
На этой странице я расскажу об одном популярном классе задач, которые встречаются в любых учебниках и методичках по теории вероятностей - задачах про бросание монет (кстати, они встречаются в части В6 ЕГЭ). Формулировки могут быть разные, например "Симметричную монету бросают дважды..." или "Бросают 3 монеты ...", но принцип решения от этого не меняется, вот увидите.
найти вероятность, что при бросании монеты
Кстати, сразу упомяну, что в контексте подобных задач не существенно, написать "бросают 3 монеты" или "бросают монету 3 раза", результат (в смысле вычисления вероятности) будет один и тот же (так как результаты бросков независимы друг от друга).
Для задач о подбрасывании монеты существуют два основных метода решения, один - по формуле классической вероятности (фактически переборный метод, доступный даже школьникам), а также его более сложный вариант с использованием комбинаторики, второй - по формуле Бернулли (на мой взгляд он даже легче первого, нужно только запомнить формулу). Рекомендую по порядку прочитать про оба метода, и потом выбирать при решении подходящий.
Объяснение:
1)x²=0
X=0
2)x(5-2x)=0
[ x=0[x=0
[ 5-2x=0 [x=2.5
3)Объяснение:
А остальные Сейчас отправлю