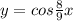
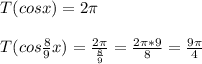
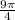
раз по условию задачи корни уравнения противоположны, то
(-b+корень из дискриминанта)/2a = - (-b-корень из дискриминанта)/2a
получается -b = b, следовательно b = 0
в нашем случае b это pp-9
pp-9=0, следовательно p = 3 или p = -3
допустим p = 3, тогда
6xx - 15 + 2 = 0
6xx = 13
x = +-корень из (13/6)
допустим p = -3, тогда
6xx + 15 + 2 = 0
6xx = -17
т.е. х получается комплексное число (я не знаю в каком сейчас классе их изучают)
значит скорей всего допустимое только p = 3, и х = +-корень из (13/6)
(х+2)(х-3)(х+1)(х-4)+4=0
конечно идеально. где есть 2 4 8 16 ... скобок сделать замена среднего арифметического (x+2+x-3+x+1+x-4)/4 = x - 1 и тогда будут просто перемножение двух квадратов и констант
можно по другому
[(х+2)(x-4)]*[(х-3)(х+1)]+4=0
(x^2 + 2x - 4x - 8)(x^2 - 3x + x - 3) + 4 = 0
(x^2 - 2x - 8)(x^2 - 2x - 3) + 4 = 0
x^2 - 2x - 3 = t
x^2-2x - 8 = t - 5
t(t-5) + 4 = 0
t^2 - 5t + 4 = 0
D=25 - 16 = 9
t12=(5+-3)/2 = 1 4
1/ x^2 - 2x - 3 = t
x^2 - 2x - 3 = 1
x^2-2x-4 = 0
D=4+16 = 20
x12=(2+-√20)/2 = (2+-2√5)/2 = 1+-√5
2/ x^2 - 2x - 3 = t
x^2 - 2x - 3 = 4
x^2 - 2x - 7 = 0
D=4 + 28 = 32
x34=(2 +- √32)/2 = (2+-4√2)/2 = 1 +- 2√2
ответ 1 +- 2√2 1+-√5