Но мы представим 1 как дробь , такое действие еще называют домножением на сопряжённое
3 Соберем все в одну дробь
4 Заметим в знаменателе разность квадратов
где
5 Упростим знаменатель
6 Представим дробь как произведение7 Представим предел произведения как произведение пределов8 Посчитаем первый предел9 Так как то мы можем заметить в пределе на 10 Умножим выражение пол пределом на 1
Но 1 мы представим в виде
11 Вынесем константу (3) за предел
12 Имеем первый замечательный предел, он равен 1ОТВЕТ
Что значит решить систему линейных уравнений? Решить систему уравнений – это значит найти множество её решений. Решение системы представляет собой набор значений всех входящих в неё переменных, который обращает КАЖДОЕ уравнение системы в верное равенство. Кроме того, система может быть несовместной (не иметь решений). Не тушуйтесь, это общее определение =) У нас же будет всего лишь одно значение «икс» и одно значение «игрек», которые удовлетворяют каждому уравнению с-мы.Существует графический метод решения системы, с которым можно ознакомиться на урокеПростейшие задачи с прямой. Там же я рассказал о геометрическом смысле системы двух линейных уравнений с двумя неизвестными. Но сейчас на дворе эра алгебры, и числа-числа, действия-действия.
Но мы представим 1 как дробь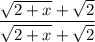 , такое действие еще называют домножением на сопряжённое
, такое действие еще называют домножением на сопряжённое
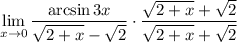
3 Соберем все в одну дробь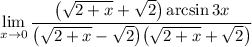
4 Заметим в знаменателе разность квадратов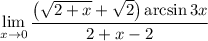
5 Упростим знаменатель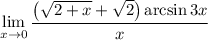
6 Представим дробь как произведениеНо 1 мы представим в виде
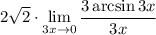
11 Вынесем константу (3) за предел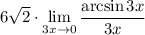
12 Имеем первый замечательный предел, он равен 1