1) x∈(1;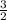 
)
2) x∈(-∞; -3)∪(1; +∞)
Объяснение первого неравенства:
Чтобы произведение было меньше нуля, множители должны иметь разные знаки. Тогда получаем две системы (знака системы сайт не имеет, строчки должны быть объединены фигурной скобкой).
Первая:
x-1<0
2x-3>0
Вторая:
x-1>0
2x-3<0
Решение первой:
x-1<0
x<1;
2x-3>0
2x>3
x>;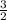
Поскольку мы решали систему, нужно найти пересечение решений. Здесь пересечение - пустое множество, потому что 3/2 больше 1.
Решение второй:
x-1>0
x>1;
2x-3<0
2x<3
x<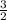
Пересечение решений - x∈(1; 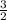) (скобки ставим круглые, потому что знак неравенства строгий)
Объяснение второго неравенства:
Чтобы произведение было больше нуля, множители должны иметь один знак. Тогда получаем две системы:
Первая:
x+3>0
x-1>0
Вторая:
x+3<0
x-1<0
Решение первой:
x+3>0
x>-3;
x-1>0
x>1;
Пересечение: x∈(1; +∞)
Решение второй:
x+3<0
x<-3;
x-1<0
x<1;
Пересечение: x∈(-∞; -3)
Пересекаем решения первой и второй систем и получаем: x∈(-∞; -3)∪(1; +∞)
log a (a^2/b) log a (a^2) - log a (b)
5log (b^2)/a (a^2/b)= 5· = 5· =
log a (b^2)/a log a (b^2)-log a (a)
2- 3 (-1)
= 5 = 5 = -1
2·3 -1 5
2) log 2 (a^1/3) , если log 4 (a^3)=9
log 4 (a^3)=9 ⇔3 log 4 (a)=9 ⇔ log 4 (a)=3
log 4 (a^1/3) (1/3)log 4 (a) 1log 2 (a^1/3) = = = = 2
log 4 (2) log 4 (√4) 1/2
3) lg2.5 если log 4(125) = a
log 4(125) = a ⇔ log 4(5³) =3 log 4(5) =a ⇔ log 4(5)=a/3
log 4 (5/2) log 4 (5)-log 4 (2) a/3-1/2 2a-3lg2.5 = = = =
log 4 (5·2) log 4 (5) +log 4 (2) a/3 +1/2 2a+3