Дана арифметическая прогрессия -15, -12, ..., то есть a₁= -15, a₂= -12. Тогда
а) её разность:
d = a₂ - a₁ = -12 - (-15) = -12 + 15 = 3.
б) формула n-члена этой прогрессии :
a(n) = -15+3·(n-1)
в) выясним, содержится ли в этой прогрессии число 12:
a(n) = 12 или
-15+3·(n-1) = 12
3·(n-1) = 12 + 15
3·(n-1) = 27
n-1 = 27:3
n = 9+1=10∈N
Содержится под номером 10.
г) Так как d=3 >0, то в этой прогрессии бесконечное количество положительных членов. В самом деле:
a(n) = -15+3·(n-1)>0
3·(n-1)>15
n-1>15:3
n>5+1
n>6
Начиная с 7-члена арифметической прогрессии все члены положительные. Так как множество натуральных чисел N бесконечно, то положительных членов арифметической прогрессии бесконечно.
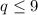
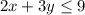
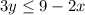
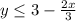
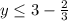
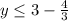
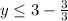
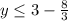
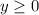
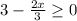

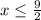
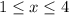
-27+40√5
Объяснение:
(√5+7√2)(7√2-√5)-(10-2√5)²=
=(7√2+√5)(7√2-√5)-(10-2√5)²=
=(7√2)²-(√5)²-(10²-2*10*2√5+(2√5)²)=
=49*2-5-(100-40√5+20) =
=98-5-100+40√5-20=
=-27+40√5
Комментарии к решению:
a+b=b+a
(a+b)(a-b)=a²-b²
(a-b)²=a²-2ab+b²