Объяснение:
Натуральные числа
Понятие натурального числа, вызванное потребностью счёта предметов, возникло ещё в доисторические времена. Процесс формирования понятия натурального числа протекал следующим образом. На низшей ступени первобытного общества понятие отвлеченного числа отсутствовало. Это не значит, что первобытный человек не мог отдавать себе отчёта о количестве предметов конкретно данной совокупности, например о количестве людей, участвующих в охоте, о количестве озёр, в которых можно ловить рыбу, и т.д. Но в сознании первобытного человека ещё не сформировалось то общее, что есть в объектах такого рода, как например, «три человека», «три озера» и т.д. Анализ языков первобытных народностей показывает, что для счёта предметов различного рода употреблялись словесные обороты. Слово «три» в контекстах «три человека», «три лодки» передавались различно. Конечно, такие именованные числовые ряды были очень короткими и завершались индивидуализированным понятием («много») о большом количестве тех или других предметов, которое тоже являлось именованным, то есть выражалось разными словами для предметов разного рода, такими , как «толпа», «стадо», «куча» и т.д.
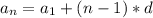
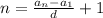
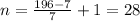
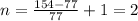
1 задача
a= 10cм
в= 6см
P= 32cм
2 задача
6 км/ч или км/ч
Объяснение:
1 задача
S=60см2
(х+4)х=60
2х+4х=60
х=10
то есть первая сторона=10см, а вторая 10-4=6 см
Периметр
(6+10)2=32 см.
2 задача
х км/ч скорость лодки при движении по озеру
(х-2) км/ч скорость лодки против течения реки
6/(х-2) ч плыл турист на лодке против течения реки
15/х ч плыл турист на лодке по озеру
Так как турист затратил на путь по озеру на 1 ч больше чем на путь по реке, то составляем уравнение
15/х - 6/(х-2) =1 общий знаменатель х(х-2).
15(х-2) -6х = х(х-2)
х² -11х +30 =0
Д = 121 -120 =1
х= (11± 1)/2
х₁ = 6 и х₂ = 5
ответ 6км/ч или 5км/ч