97,5
Объяснение:
Данная задача решаема через систему уравнения:
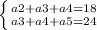
Решим эту систему при метода вычитания:
a3+a4=18-a2
a3+a4+24-a5
24-a5=18-a2
6-a5+a2=0
a5-a2=6 - данное выражение показывает нам разницу между членами прогресcии через a3 и a4
Разница между ближайшими членами d = 1,5 ,потому-что согласно a5-a2=6
Теперь есть формула:
a2=a1+d => d=1,5 => a2=a1+d ,тогда подставим в первое уравнение системы:
a1+1,5+a3+a4=18
Но при этом а3=a1+3 и а4=а1+4,5
Тогда:
a1+1,5+a1+3+а1+4,5=18
3*a1+9=18
a1=3
Находим все члены и их сумма равна:
3+4,5+6+7,5+9+10,5+12+13,5+15+16,5=97,5
ответ: 97,5
(В решении или в вычислениях могу ошибаться!)
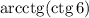
Известно соотношение:
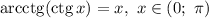
Кроме этого, известно, что основной период котангенса равен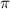 
:
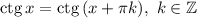
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида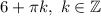 
, чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
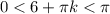
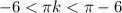
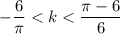
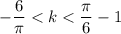
Выполним оценку обеих частей неравенства:
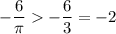
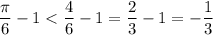
Получим:
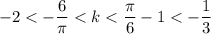
Или записывая соотношение для k:
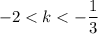
Единственное подходящее целое значение: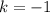 
.
Запишем:
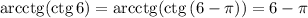
Действительно, 
, арккотангенс может принимать такое значение.
ответ: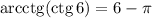 
ответ:0.88
Объяснение:
используем формулы а²-с²=(а-с)(а+с)
а²+2ас+с²=(а+с)²
(47²-3²)/(27²+2*27*13+13²)=(47-3)*(47+3)/(27+13)²=44*50/50²=44/50=0.88