Каким бы мы не решали, стоит разложить выражение на множители.
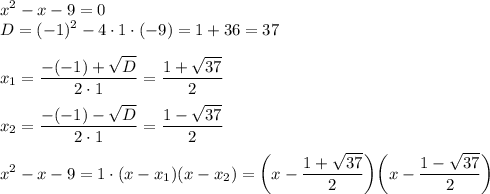
Тогда имеем: 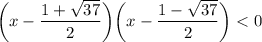
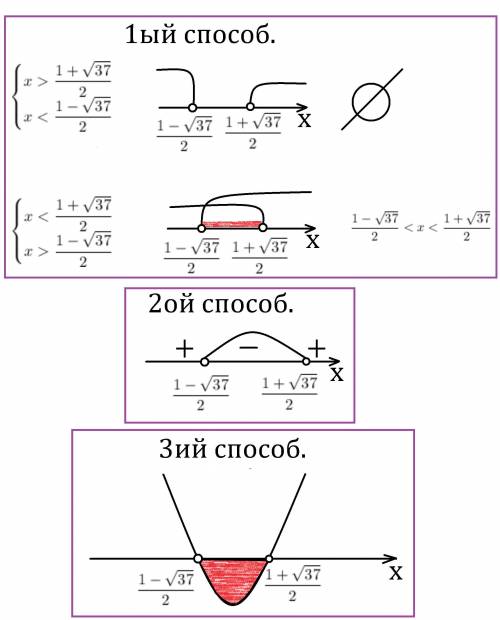
1ый через знак множителей):
Произведение будет отрицательным, если один из множителей отрицательный, а другой положительный.
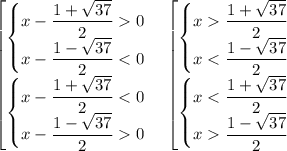
ответ: 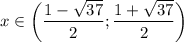
2ой метод интервалов):
Отмечаем на координатной прямой точки, в которых выражение обращается в ноль. И выкалываем их т.к. неравенство строгое (<, а не ≤). Мы получили 3 интервала. Перед множителями знак положителен, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (нету чётных степеней, где знак может не измениться). Нас интересует, когда меньше, поэтому выбираем интервалы с минусом.
ответ: 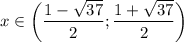
3ий графический):
y = x²-x-9
Это парабола, ветви которой направлены вверх. У функции есть два нуля:
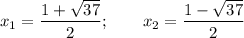 . Нас интересует, когда меньше нуля, это когда график ниже оси Ox.
. Нас интересует, когда меньше нуля, это когда график ниже оси Ox.
ответ: 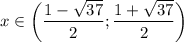
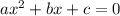 где коэффициенты
где коэффициенты 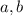 и
и  соответственно
соответственно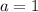 ,
, 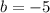 и
и 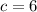
 при
при 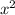 равен 1, единица больше 0, сл, ветви параболы будут направлены вверх
равен 1, единица больше 0, сл, ветви параболы будут направлены вверх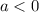 ветви будут направлены вниз)
ветви будут направлены вниз) обозначается как
обозначается как 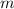 и считается по формуле
и считается по формуле 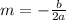
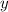 обозначается
обозначается 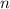 и ищется путем подстановки числа
и ищется путем подстановки числа 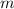 в уравнение вместо
в уравнение вместо 
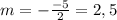
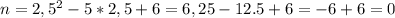
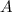 вершины параболы имеет координату (2,5;0)
вершины параболы имеет координату (2,5;0)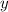
 и
и 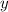
 находятся при, при
находятся при, при 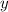 = 0
= 0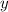 - когда
- когда  = 0
= 0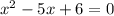
 то есть 6
то есть 6 в уравнение и найти относящиеся к ним
в уравнение и найти относящиеся к ним 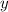 - это и будут координаты точек, через которые проходит график
- это и будут координаты точек, через которые проходит график
882.681788297
Объяснение: