Question

При каких значениях параметр а значение интеграла максимален?

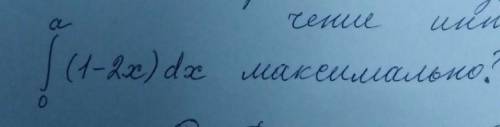
Answer 1

$\boxed{a = 0,5}$

Объяснение:

$max: \displaystyle \int\limits^a_0 {(1 - 2x)} \, dx$

Введем функцию: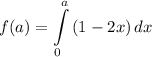 $f(a) = \displaystyle \int\limits^a_0 {(1 - 2x)} \, dx$

Неопределенный интеграл:  

$\displaystyle \int {(1 - 2x)} \, dx = \displaystyle \int {1 \cdot} \, dx - \displaystyle \int { 2x} \, dx = \displaystyle \int {1 \cdot} \, dx - \displaystyle 2 \int {x} \, dx = x + C_{1} - 2 \cdot \dfrac{x^{2}}{2} + C_{2}=$

$= x - x^{2} + C$

$F(x) = x - x^{2} + C$ - первообразная для функции $g(x) = (1 - 2x)$

$f(a) = \displaystyle \int\limits^a_0 {(1 - 2x)} \, dx = \displaystyle \int\limits^a_0 {g(x)} \, dx = F(a) - F(0) = a - a^{2} + C - 0 - 0^{2} - C =$

$= a - a^{2}$

Найдем максимум функции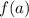 $f(a)$:

$f'(a) = (a - a^{2})' = 1 - 2a$

$f''(a) = (f'(a))' = (1 - 2a)' = -2$

$f''(a) < 0$ следовательно функция $f(a)$ имеет максимум

(при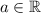 $a \in \mathbb R$)

$f'(a) = 0$

$1 - 2a = 0$

$2a = 1|:2$

$a = 0,5$

То есть максимум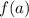 $f(a)$ при $a = 0,5$

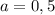
Условие:

При каком значении a значение интеграла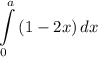 $\displaystyle \int\limits^a_0 {(1 - 2x)} \, dx$ максимально?

Ключевые слова:

Интегралы, определенный интеграл, интеграл с параметром, экстремумы функции, максимум функции