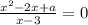cos5x + cosx + 2cos2x = 0
2cos(5x+x/2)cos(5x-x/2) + 2cos2x = 0
2cos(6x/2)cos(4x/2) + 2cos2x = 0
2cos3x × cos2x + 2cos2x = 0
2cos2x × (cos3x + 1) = 0 | : 2
cos2x × (cos3x + 1) = 0
cos2x = 0 или cos3x + 1 = 0
2x = π/2 + πn cos3x = -1
x₁ = π/2 × 1/2 + πn × 1/2 3x = π + 2πn
x₁ = π/4 + πn/2, n∈Z x₂ = π × 1/3 + 2πn × 1/3
x₂ = π/3 + 2πn/3, n∈Z
ответ: x₁ = π/4 + πn/2, n∈Z
x₂ = π/3 + 2πn/3, n∈Z
Задание 4.
В задании явно видна развернутая формула суммы кубов, которую, для удобства, можно свернуть
Сумма кубов -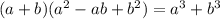 
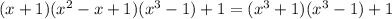
Теперь просто раскрываем скобки (можно воспользоваться формулой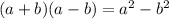 
, но при этом надо знать что x будет в степени 3 · 2; чтобы не усложнять решение и не запутывать его, раскрою скобки не по формуле)
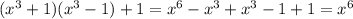
ответ: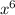 
.
Задание 5.
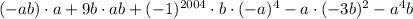
Если степень чётная, то числа в этой скобке при раскрытии, даже со знаком минус, становятся положительным и в степени, стоявшей после скобки.
Таким образом, (-ab) будет иметь нечётную (первую) степень и раскроется как -ab;
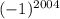будет иметь четную степень и раскроется как 1 (при умножении 1 на любое кол-во раз получается 1);
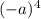будет иметь четную степень и раскроется как 
;
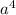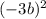раскроется как 
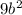(мы умножаем каждую букву и число в скобке)
Получаем
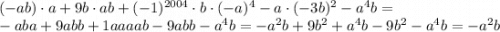
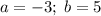
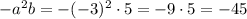
ответ: -45.
имеет единственный корень.
a = 1
Объяснение:
Дано уравнение
Найдём значение параметра a, при котором уравнение имеет единственный корень
Наложим условие, что x ≠ 3 и опустим знаменатель
x² - 2x + a = 0
Для того, чтобы у уравнения был единственный корень, необходимо и достаточно, чтобы дискриминант уравнения равнялся нулю
D = 2² - 4a = 0
4 - 4a = 0
4 = 4a
a = 1
Подставим это значение в уравнение
x² - 2x + 1 = 0
(x - 1)² = 0
x = 1
Это не противоречит условию, наложенному на знаменатель, значит a = 1