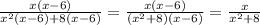
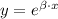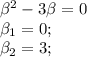
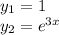
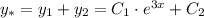
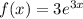
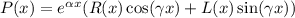.
, где R(x) и S(x) - полиномы, которое имеет частное решение.
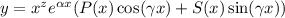, где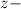 
кратность корня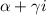 
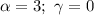
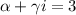является корнем характеристического уравнения кратности z=1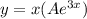
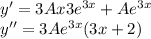
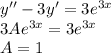
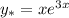
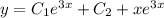
В решении.
Объяснение:
Решить уравнение:
1/(х - 4)² - 7/(х - 4) + 10 = 0
Умножить все части уравнения на (х - 4)², чтобы избавиться от дробного выражения:
1 - 7*(х - 4) + 10*(х - 4)² = 0
Разложить квадрат разности по формуле:
1 - 7*(х - 4) + 10*(х² - 8х + 16) = 0
Раскрыть скобки:
1 - 7х + 28 + 10х² - 80х + 160 = 0
Привести подобные:
10х² - 87х + 189 = 0, квадратное уравнение, ищем корни:
ОДЗ: х ≠ 4;
D=b²-4ac = 7569 - 7560 = 9 √D=3
х₁=(-b-√D)/2a
х₁=(87-3)/20
х₁=84/20
х₁=4,2;
х₂=(-b+√D)/2a
х₂=(87+3)/20
х₂=90/20
х₂=4,5.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
