Пусть за час 1-й кран будет наполнять весь бассейн
за час 2-й кран будет наполнять бассейн.
Если 1 - это объем всего бассейна, тогда
- объем воды, который проходит через 1-й кран за 1 час.
- объем воды, который проходит через 2-й кран за 1 час.
- общая производительность двух кранов.
- первое уравнение
- второе уравнение
Из первого уравнения получим: и вставим во второе уравнение:
Подставим в первое уравнение:
ответ: за 3 часа 1-й кран наполнит весь бассейн;
за 6 часов 2-й кран наполнит весь бассейн.
Пусть за час 1-й кран будет наполнять весь бассейн
час 1-й кран будет наполнять весь бассейн
за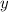 час 2-й кран будет наполнять бассейн.
час 2-й кран будет наполнять бассейн.
Если 1 - это объем всего бассейна, тогда
Из первого уравнения получим: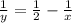 и вставим во второе уравнение:
и вставим во второе уравнение:
Подставим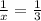 в первое уравнение:
в первое уравнение:
ответ: за 3 часа 1-й кран наполнит весь бассейн;
за 6 часов 2-й кран наполнит весь бассейн.