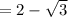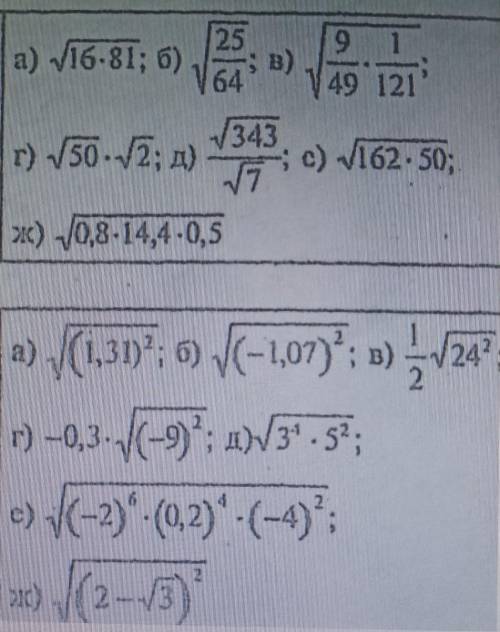
у=2х-7 искомое уравнение.
Объяснение:
Составьте уравнение вида y = kx+ b, график которого проходит через данные точки C (-3;-13) и D (1;-5)
Формула, при которой можно построить уравнение прямой по двум точкам:
(х-х₁)/(х₂-х₁)=(у-у₁)/(у₂-у₁)
C (-3;-13) и D (1;-5)
х₁= -3 у₁= -13
х₂=1 у₂= -5
Подставляем данные в формулу:
(х-(-3)/(1-(-3)=(у-(-13)/(-5)-(-13)
(х+3)/4=(у+13)/8 перемножаем крест-накрест, как в пропорции:
8(х+3)=4(у+13)
8х+24=4у+52
-4у= -8х+52-24
-4у= -8х+28
4у=8х-28/4
у=2х-7 искомое уравнение.
Середній рівень
У нас є дві точки: A (-1; 1) і B (1; 0).
Запишемо рівняння прямої і підставимо значення координат цих точок.
y = kx + b - У стандартному вікні рівняння прямої.
Підставами координати точки A:
1 = -k + b
Підставами координати точки B:
0 = k + b
Отримуємо систему рівнянь:
1 = -k + b
0 = k + b
Складемо рівняння:
1 + 0 = -k + b + k + b
1 = 2b
b = 0,5
Підставами в уже готове рівняння 0 = k + b знайдене b:
0 = k + 0,5
k = -0,5
Тепер підставимо відомі k і b в рівняння прямої:
y = -0,5x + 0,5 - Відповідь
Без підставим неяк. Можна кращу відповідь?
a) =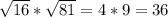
б) =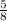
в) =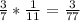
г) =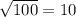
д)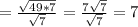
е)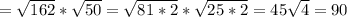
ж)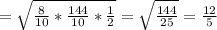
a)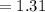
б)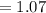
в)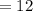
г)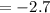
д)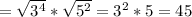
е)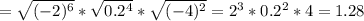
ж)