амазонка считается самой быстрой рекой. определи скорость её течения на заданном участке, если известно, что катер, собственная скорость которого равна 18 км/ч по течению 62 км, а потом против течения 15 км, затратив на весь путь 5 часов
Область допустимых значений (ОДЗ): x≠3 (иначе в знаменателе будет 0). Находим точки, в которых неравенство обращается в равенство. Рассматриваем поведение в окрестности точки х=2, для чего вычисляем значение функции при х=1.9 и х=2.1, подставляя эти значения в исходное выражение. Осталось проверить, что происходит со знаком функции после точки х=3, составляющей ОДЗ. Анализируя знаки на участках (-∞;2]; [2;3); (3;∞) мы видим, что только знак у2, соответствует знаку исходного неравенства, т.е. ответом будет [2;3)
Область допустимых значений (ОДЗ): x≠3 (иначе в знаменателе будет 0). Находим точки, в которых неравенство обращается в равенство. Рассматриваем поведение в окрестности точки х=2, для чего вычисляем значение функции при х=1.9 и х=2.1, подставляя эти значения в исходное выражение. Осталось проверить, что происходит со знаком функции после точки х=3, составляющей ОДЗ. Анализируя знаки на участках (-∞;2]; [2;3); (3;∞) мы видим, что только знак у2, соответствует знаку исходного неравенства, т.е. ответом будет [2;3)
ответ: Скорость течения реки Амазонка равна 13 км/ч
Объяснение:
Пусть скорость течения равна x-су то тогда
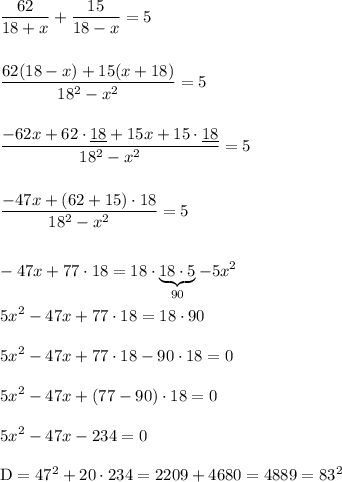
Скорость катера по течению v₁ = x+18 , против течения v₂= 18-x
По течению катер 62 км , а против течения 15 км
На весь путь затратили 5 часов
То есть
Берем корень x = 13 , так как скорость течения не может быть отрицательной