Подставим х=8, у=0 в выражение у=ах²+bx+c получим 0=а·8²+b·8+c 64a+8b+c=0
Наименьшее значение в вершине параболы, при условии, что ветви параболы направлены вверх, при этом а > 0 абсцисса вершины: х₀=-b/2а ⇒ 6=-b/2a ⇒-b=12a ⇒ b=-12a y₀=a·6²+b·6+c ⇒ -12=36a+6b+c Решаем систему трех уравнений с тремя неизвестными: { 64a+8b+c=0 ⇒ 64 a + 8· (-12a)+c=0 -32a + c= 0 (*) { b=- 12a { -12=36a+6b+c ⇒ 36a +6·(-12a)+c=-12 -36a +c= -12 (**)
Биквадратное уравнение.
Решается заменой переменной:
Если D >0, т.е.
уравнение имеет корни:
Обратный переход:
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:
0=1 - неверно, нет таких значений а
Аналогично
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:
0=1 - неверно, нет таких значений а
Если , т.е
, т.е 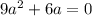
При
уравнение принимает вид:
уравнение не имеет корней
При
уравнение принимает вид:
Уравнение 4-ой степени, значит
О т в е т. При