A) 443 002,08
b) −15 606 226 225
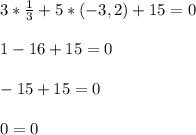
рассмотрим наше уравнение:
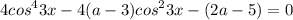
выполним замену cos²3x=t; t≥0
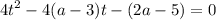
чтобы уравнение имело хотя бы один корень надо чтобы D≥0
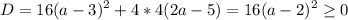
Это неравенство выполняется для любых a
тогда проверим корни, необходимо чтобы t≥0
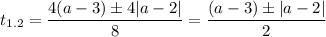
рассмотрим первый корень
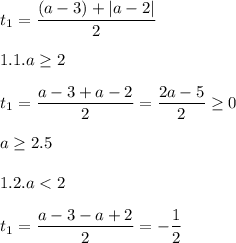
значит при а≥2.5 мы получим один положительный корень (относительно t)
проверим второй корень
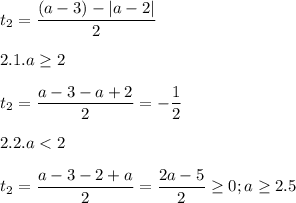
тут положительных корней не получим.
значит рассмотрим один положительный корень t=(2a-5)/2. при а≥2,5
выполним обратную замену
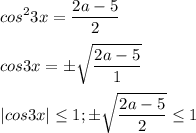
рассмотрим положительный корень
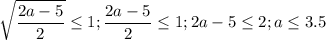
рассмотрим отрицательный корень
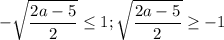
выполняется для всех а≥2.5
Собираем все вместе 2,5≤а≤3,5
а) 76²*76.58 +26²=(38²*76,58+13²)*2²=(76,58*1444+169)*4=110750,52*4=443002,08;
b)175²-95²*1315²-35²=175²-124925²-1225=-124750*125100-1225=-15606226225;