3360
Объяснение:
В слове ИНСТИТУТ 8 букв, но среди них есть повторяющиеся буквы, а именно
И - 2 раза
Т - 3 раза
Тогда количетсво перестановки букв такое:
На первое место мы поставим одну из 8 букв
На второе - одну из 7 оставшихся
На третье - одну из 6 оставшихся
......
и так далее до 1.
Так как выбор одной буквы зависит от выбора других, то нам необходимо все перемножить

Но так как были повторяющиеся буквы, мы могли одну и ту же букву посчитать несколько раз, то нам необходимо посчитать количество перестановок всех повторяющихся букв, и поделить на их количество. так как считали мы их зря.
Для буквы И: 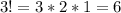
Для буквы Т: 
Делим на их произведение, получаем
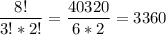
f`(x)=(4-2x)`=(4)`-(2x)`=0-2·(x)`=-2·1=-2
Применили правила:
производная суммы( разности) равна сумме( разности) производных
Производная постоянной (C)`=0
Постоянный множитель можно вынести за знак производной
(х)`=1
Производная принимает во всех точках одно и то же значение (-2)
f`(0,5)=f`(-3)=-2
в) f(x)=3x-2
f`(x)=(3x-2)`=(3х)`-(2)`=3·(x)`-0=3·1=3
Применили правила:
производная суммы( разности) равна сумме( разности) производных
Производная постоянной (C)`=0
Постоянный множитель можно вынести за знак производной
(х)`=1
Производная принимает во всех точках одно и то же значение (3)
f`(5)=f`(-2)=3