В решении.
Объяснение:
1. Решить систему неравенств:
х² - 4х < 0
x² - x - 6 >= 0
Решить первое неравенство:
Приравнять к нулю и решить квадратное уравнение:
х² - 4х = 0
х(х - 4) = 0
х₁ = 0;
х - 4 = 0
х₂ = 4;
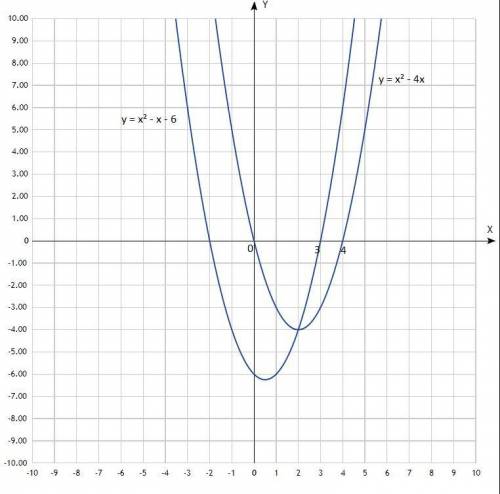
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х=0 и х=4.
у < 0 (как в неравенстве) при х от 0 до х=4, график ниже оси Ох.
Решения неравенства: х∈(0; 4).
Неравенство строгое, скобки круглые.
Решить второе неравенство:
Приравнять к нулю и решить квадратное уравнение:
x² - x - 6 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 1 + 24 = 25 √D=5
х₁=(-b-√D)/2a
х₁=(1-5)/2
х₁= -4/2
х₁= -2;
х₂=(-b+√D)/2a
х₂=(1+5)/2
х₂=6/2
х₂=3;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -2 и х=3.
у >= 0 (как в неравенстве) при х от -∞ до х= -2 и от х=3 до +∞, график выше оси Ох.
Решения неравенства: х∈(-∞; -2]∪[3; +∞).
Уравнение нестрогое, скобка квадратная, а знаки бесконечности всегда под круглой скобкой.
Отметить на числовой оси схематично решения неравенств:
-∞ -2 0 3 4 +∞
Точки х= -2 и х = 3 - закрашенные.
Пересечение решений: х∈[3; 4) (двойная штриховка).
Решения системы неравенств: х∈[3; 4).
2. Решить систему неравенств:
4х² - 1 > 0
2x² - 5x + 3 < 0
Решить первое неравенство:
Приравнять к нулю и решить квадратное уравнение:
4х² - 1 = 0
4х² = 1
х² = 1/4
х = ±√1/4
х = ±1/2 = ±0,5;
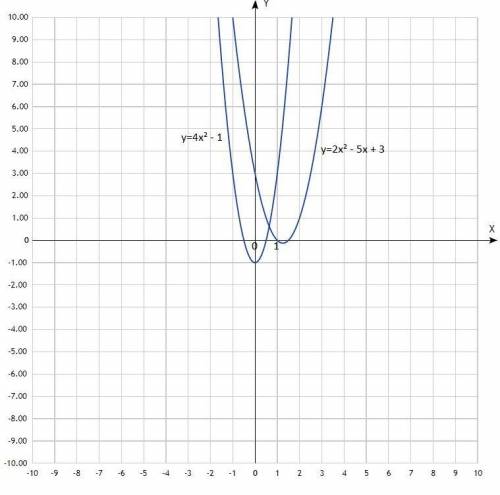
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -0,5 и х=0,5.
у > 0 (как в неравенстве) при х от -∞ до х= -0,5 и от х=0,5 до +∞, график выше оси Ох.
Решения неравенства: х∈(-∞; -0,5)∪(0,5; +∞).
Неравенство строгое, скобки круглые.
Решить второе неравенство:
Приравнять к нулю и решить квадратное уравнение:
2x² - 5x + 3 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 25 - 24 = 1 √D=1
х₁=(-b-√D)/2a
х₁=(5-1)/4
х₁=4/4
х₁=1;
х₂=(-b+√D)/2a
х₂=(5+1)/4
х₂=6/4
х₂=1,5;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х=1 и х=1,5.
у < 0 (как в неравенстве) при х от 1 до х=1,5, график ниже оси Ох.
Решения неравенства: х∈(1; 1,5).
Неравенство строгое, скобки круглые.
Отметить на числовой оси схематично решения неравенств:
-∞ -0,5 0,5 1 1,5 +∞
Пересечение решений: х∈(1; 1,5) (двойная штриховка).
Решения системы неравенств: х∈(1; 1,5).
РЕШЕНИЕ
1.
Всего событий - n.
N(A) = 8 - благоприятных для А - дано.
N(B) = n - N(A) = 17 - 8 = 9 - благоприятных для В - ОТВЕТ
р(А) = 0,32 - вероятность А - дано.
р(В) = 1 - 0,32 = 0,68 - вероятность события В - ОТВЕТ
2.
Всего вариантов на кости - граней - n =6.
Событие А - выпало четное - A={2,4,6} - m(А) = 3
Событие В - больше 3 - B={4,5,6} - m(B) = 3
Событие АВ - пересечение множеств А∩В = {4;6} - m(AB) = 2.
Вероятность АВ по классической формуле
p(AB) = m(AB)/n = 2/6 = 1/3 - вероятность - ОТВЕТ (≈33,3%)
3.
Всего для каждого броска вариантов - n = 6.
Событий А - меньше 3 - A={1,2} - m(A) = 2, p(A) = 2/6 = 1/3
Событие В - больше 4 - B={5,6} - m(B) = 2, p(B) = 2/6 = 1/3
Элементарные события:
1,5 и 1,6 и 2,5 и 2,6 - четыре варианта.
Событие А*В - "И" А "И" В - произведение вероятностей каждого.
p(A*B) = 1/3 * 1/3 = 1/9 - вероятность - ОТВЕТ (≈11,1%)
ИЛИ
Для двух бросков = n = 6² = 36, m(AB) = 4, p(A*B) = 4/36 = 1/9 - ОТВЕТ
4.
Вероятность несовместных событий ("ИЛИ") равна сумме вероятностей каждого - называется "ИЛИ" U "ИЛИ" V.
Р(U+V) = р(U)+р(V) = 0,3 + 0,5 = 0,8 - вероятность - ОТВЕТ