ответ: радиус равен 28
Объяснение:
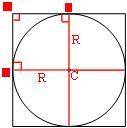
Проведем радиусы окружности к точкам касания со сторонами квадрата, как показано на рисунке. Обозначим ключевые точки A, B, C и D. ABCD образует четырехугольник. В этом четырехугольнике: ∠A=90° (по определению квадрата). ∠B=∠D=90° (по свойству касательной). Тогда и ∠С=90° (так как сумма углов четырехугольника равна 360°). Т.е. ABCD - прямоугольник (по определению). По свойству прямоугольника: AB=CD=R AD=BD=R Т.е. ABCD - квадрат. Из рисунка очевидно, что радиус равен половине стороны квадрата: R=56/2=28
Объяснение:
1. Преобразуйте в многочлен:
1) (a + 4)²=a²+8a+16 2) (3у - с)²=9y²-6cy+c²
3) (2a - 5)( 2a + 5) =4a²-25 4) (x² + y)( x² - y)=x^4-y²
2. Разложите на множители:
1) 0,36 – с²=(0,6-c)(0,6+c) 2) 5a² + 10a=5a(a+2)
3) 16x² – 49=(4x)²-7²=(4x-7)(4x+7)
3) Упростите выражение: (m - 1)(т + 1) - (т - 3)=mt-2t+m+2
4. Выполните действия:
a) 3(1 + 2xy)( 1 - 2xy) =3(1-4x²y²)=3-12x²y² б) (x²-y)=(x-√y)(a+√y)
5. Решите уравнение: (x - 2)(x + 2) - x(x + 5) = - 8
X²-4-x²-5x=-8
-5x=-4
X=4/5=0,8
(a-3)^2=(a+8)(a-8)
а^2-6а+9=а^2-64
-6а=-64-9
-6а=-73
а=73:6=12 1/6