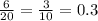Выпишем все двузначные квадраты: 16, 25, 36, 49, 64, 81. Если это число начиналось с 1, то первые цифры только 16, значит 2-я и 3-я цифры - 64, после этого (3-я и 4-ая) может быть только 49. Дальше продолжать не можем, потому что нет двузначных квадратов, начинающихся с 9. Итак, максимальное число начинающееся с 1 и удовлетворяющее условию 1649 Аналогично для 2 получаем 25, т.к. на 5 двузначных квадратов нет. И т.д.: Начинающееся на 3: 3649 на 4: 49 на 5 - таких чисел нет на 6: 649 на 7: - таких нет, т.к. нет двузначных квадратов начинающихся с 7. на 8: - 81649 на 9: - нет. Итак, наибольшее: 81649.
Выпишем все двузначные квадраты: 16, 25, 36, 49, 64, 81. Если это число начиналось с 1, то первые цифры только 16, значит 2-я и 3-я цифры - 64, после этого (3-я и 4-ая) может быть только 49. Дальше продолжать не можем, потому что нет двузначных квадратов, начинающихся с 9. Итак, максимальное число начинающееся с 1 и удовлетворяющее условию 1649 Аналогично для 2 получаем 25, т.к. на 5 двузначных квадратов нет. И т.д.: Начинающееся на 3: 3649 на 4: 49 на 5 - таких чисел нет на 6: 649 на 7: - таких нет, т.к. нет двузначных квадратов начинающихся с 7. на 8: - 81649 на 9: - нет. Итак, наибольшее: 81649.
множество натуральных чисел до 20 - {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
a) кратным пяти из множество будет множество {5, 10, 15, 20}. Вероятность того, что из 20 возможных мы выберем именно эти 4 равна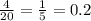
б) Делителями числа 20 будет множество {1, 2, 4, 5, 10, 20}. Вероятность того, что мы из 20 возможных выберем эти 6 равна