Первый этап. Составление математической модели.
Пусть х сторона данного квадрата, сторона нового квадрата будет равна 5х. Площадь первого квадрата будет
S₁=x² см²
Площадь нового квадрата будет
S₂=(5x)²=25x² см²
По условию площадь нового квадрата на 384 см².
Получаем уравнение: 25х²-х²=384
Второй этап. Работа с математической моделью
25х²-х²=384
24х²=384
х²=384/24
х²=16
х=+-4 - по условию подходит только х=4
Третий этап. Получение ответа на вопрос задачи.
х - сторона исходного квадрата, х=4 см, значит сторона квадрата 4 см.
ответ 4 см сторона квадрата
Прямые y=a+x и y=a-x симметричны относительно оси ординат и образуют с осью обсцисс у = 0 равнобедренный треугольник с высотой, равной а, проведенной к основанию. Каждая из этих прямых имеет угловой коэффициент, равный 1 по модулю, в первом случае +1, во втором - 1.
Половина основания полученной фигуры - равнобедренного треугольника - равна а, а боковая сторона этого треугольника равна а корней из 2.
Центр тяжести треугольника находится в точке пересечения его медиан. Высота а также является и медианой, так как треугольник равнобедренный. Абсцисса точки, являющейся центром тяжести, равно нулю (х = 0).
Медианы делятся точкой пересечения в отношении 2:1, считая от вершины. Потому ордината искомой точки равна а/3.
Таким образом, коориднаты центра тяжести искомой фигуры равны:
Абсцисса 0
Ордината а/3
ответ: (0; а/3)
3.
1)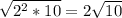
2)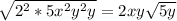
4.
1)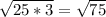
2)