Найдите сумму многочленов:(0.6a+0.2a²)+(0.2a-0.4a²) Выберите получившееся выражение.
0.8a-0.2a²
0.2a²+0.8a
0.6a²+0.8a
0.6a²
Вычислите её значение, если а=0.1

👇

Увидеть ответ

Ответ:

morfikk

04.08.2021

0.8а-0.2а²

0.8•0.1-0.2⁰′¹=0.08-0.02= 0.06

4,4(11 оценок)

Открыть все ответы

Ответ:

margaRita2281

04.08.2021

‥・Здравствуйте, Azma15! ・‥

• Решение:

Решением данного примера является ответ 5+4а³+9ab+7ac²+18a³b+14a³c²-14b+10c².

• Как и почему?

Для того, чтобы нам проверить правильность нашего решения, то мы должны составить план решения, с которого мы будем решать данный пример. Указан он будет ниже:

• 1. Сократить дробь;

• 2. Раскрыть скобки;

• 3. Изменить знаки;

• 4. Проверка ответа;

• 5. Записать ответ.

• Шаг 1: Убрать ненужные скобки.

Для того, чтобы нам сделать 1 шаг, то мы должны раскрыть скобки, то есть, убрать ненужные скобки (5+4а³).

• Шаг 2: Перемножить выражения в скобках.

Для того, чтобы нам выполнить 2 шаг, то мы должны перемножить выражения в скобках чисел (а+2а³)×(9b+7c²).

• Подробные шаги решения:

1. Умножить каждый член их первого выражения в скобках на каждый член из второго выражения в скобках;

2. Вычислить произведение чисел 2 и 9;

3. Вычислить произведения чисел 2 и 7.

• Шаг 3: Изменить знаки каждого члена в скобках.

Для того, чтобы нам решить 3 шаг, то мы должны судить так: когда перед скобками стоит знак «-», то мы должны изменить знак каждого члена в скобках, где есть знак «-».

• Шаг 4: Проверка нашего ответа.

Для того, чтобы нам проверить правильность нашего ответа, то мы должны всё выполнять по-обратному пути, то есть, с конца до начала. Если у нас в конце получился начальный ответ, то это значит, что мы решили данный пример верно. Но, а если, у нас получился какой-то нибудь другой ответ, не начальный, то это значит, что мы допустили ошибку в каком-то месте шага. Нам нужно начать всё сначала.

• Шаг 5: Записать наш конечный ответ.

А теперь, записываем конечный ответ, который у нас получился. Записывать мы будем его так (без чёрных вертикальных линий):

| 5+4а³+9ab+7ac²+18a³b+14a³c²-14b+10c²

• 〔 ! 〕Замечание: Обратите внимание на то, что в ответе у нас получилось упрощение данного выражения. Точный ответ на данный пример дать НЕЛЬЗЯ.

• Вывод: В таком случае, у нас в ответе получается решение 5+4а³+9ab+7ac²+18a³b+14a³c²-14b+10c².

‥・С уважением, Ваша GraceMiller! :) ・‥

4,4(68 оценок)

Ответ:

milankae

04.08.2021

выпишем координаты данных векторов:

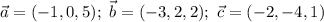
$\vec{a}=(-1,0,5);\ \vec{b}=(-3,2,2);\ \vec{c}=(-2,-4,1)$

координаты:

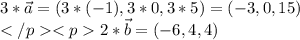
$3*\vec{a}=(3*(-1),3*0,3*5)=(-3,0,15)\\2*\vec{b}=(-6,4,4)$

скалярное произведение векторов - число:

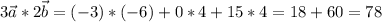
$3\vec{a}*2\vec{b}=(-3)*(-6)+0*4+15*4=18+60=78$

б)

координаты:

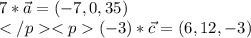
$7*\vec{a}=(-7,0,35)\\(-3)*\vec{c}=(6,12,-3)$

векторное произведение векторов - вектор, находим его координаты:

$7\vec{a}\times (-3\vec{b})=\left|\begin{array}{ccc}\vec{i} & \vec{j} & \vec{k} \\-7 & 0 & 35 \\6 & 12 & -3\end{array}\right|=\vec{i}*\left|\begin{array}{cc}0 & 35 \\12 & -3\end{array}\right|-\vec{j}*\left|\begin{array}{cc}-7 & 35 \\6 & -3\end{array}\right|+\vec{k}*\left|\begin{array}{cc}-7 & 0 \\6 & 12\end{array}\right|=\vec{i}*(-12*35)-\vec{j}*(21-6*35)+\vec{k}*(12*(-7))=\\=-420\vec{i}+189\vec{j}-84*\vec{k}=(-420,189,-84)$

находим модуль(длину) полученного вектора:

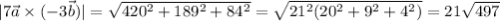
$|7\vec{a}\times (-3\vec{b})|=\sqrt{420^2+189^2+84^2}=\sqrt{21^2(20^2+9^2+4^2)}=21\sqrt{497}$

в)

координаты:

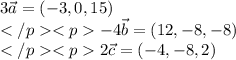
$3\vec{a}=(-3,0,15)\\-4\vec{b}=(12,-8,-8)\\2\vec{c}=(-4,-8,2)$

смешанное произведение векторов - число, находим его:

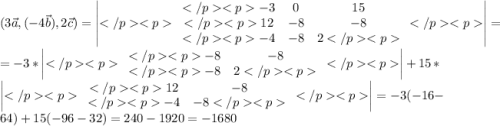
$(3\vec{a},(-4\vec{b}),2\vec{c})=\left|\begin{array}{ccc}-3 & 0 & 15 \\12 & -8 & -8 \\-4 & -8 & 2\end{array}\right|=\\=-3*\left|\begin{array}{cc}-8 & -8 \\-8 & 2\end{array}\right|+15*\left|\begin{array}{cc}12 & -8 \\-4 & -8\end{array}\right|=-3(-16-64)+15(-96-32)=240-1920=-1680$

г)

Координаты:

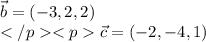
$\vec{b}=(-3,2,2)\\\vec{c}=(-2,-4,1)$

Векторы коллинеарны, если их соответствующие кординаты пропорциональны

Проверим это утверждение:

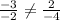
$\frac{-3}{-2}\neq \frac{2}{-4}$

Данное равенство неверно, значит векторы b и c не коллинеарны

Векторы ортогональны, если их скалярное произведение равно нулю.

Проверим это утверждение:

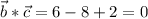
$\vec{b}*\vec{c}=6-8+2=0$

- верно, значит данные векторы ортогональны

Векторы b и c ортогональны

д)

Координаты:

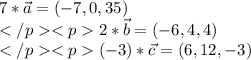
$7*\vec{a}=(-7,0,35)\\2*\vec{b}=(-6,4,4)\\(-3)*\vec{c}=(6,12,-3)$

Три вектора компланарны, если их смешанное произведение равно нулю.

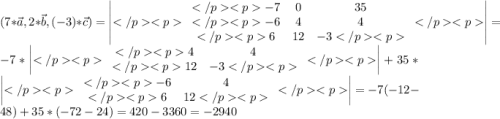
$(7*\vec{a},2*\vec{b},(-3)*\vec{c})=\left|\begin{array}{ccc}-7 & 0 & 35 \\-6 & 4 & 4 \\6 & 12 & -3\end{array}\right|=-7*\left|\begin{array}{cc}4 & 4 \\12 & -3\end{array}\right|+35*\left|\begin{array}{cc}-6 & 4 \\6 & 12\end{array}\right|=-7(-12-48)+35*(-72-24)=420-3360=-2940$