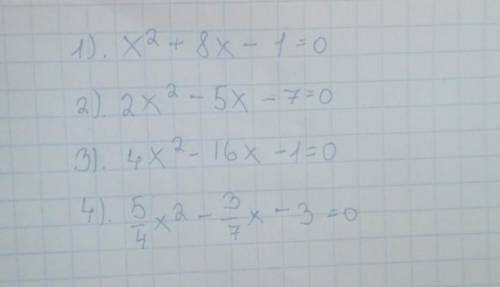
1.
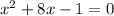
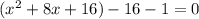
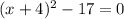
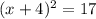
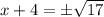
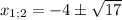
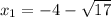
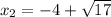
2.
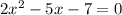
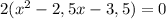
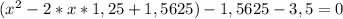

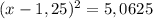
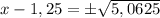
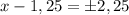
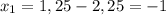
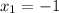
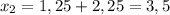
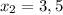
3.
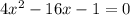
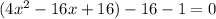
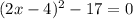
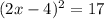

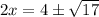
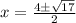
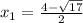
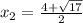
4.
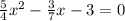
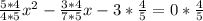
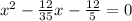
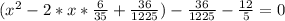
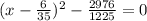
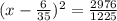
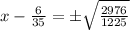
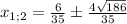
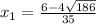
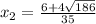
1
x^2+х-а=0 ; x^2+pх-q=0 ; p=1 ; q=a ; x1=4
теорема виета для приведенного квадратного уравнения
x1+x2 =-p = -1 ; 4+x2 = -1 ; x2 = -5
x1*x2 =q =a ; 4 *(-5) = -20
ОТВЕТ
x2 = -5
a= -20
2
x1=-5 ; x2 = 8
(x+5) (x-8) = x^2-8x+5x -40 = x^2-3x-40
5
то же самое ,что 2
3
а)
x^2/ (x+6) = 1/2 ;
ОДЗ x+6 = 0 ; x = -6 (- 6 исключаем из корней)
2x^2 = (x+6) ;
2x^2 - x- 6 =0;
D = (-1)^2 - 4*2(-6) =1+48=49 ; √D = √49 = -/+7
x1 = (1 -7 )/ (2*2)=-6/4 =-3/2 =- 1.5
x2 = (1 +7 )/ (2*2)=8/4 =2
ОТВЕТ -1.5 ; 2
б)
(x^2-x) / (x+3) = 12 / (x+3)
ОДЗ x+3 = 0 ; x = -3 (- 3 исключаем из корней)
(x^2-x) = 12
x^2-x - 12 =0
D = (-1)^2 - 4 *1*(-12)=49 ; √D = √49 = -/+7
x1 = (1-7) / 2 = -6/2 = -3 не входит в ОДЗ
x2 = (1+7) / 2 = 8/2 = 4
ОТВЕТ 4
1
x^2+х-а=0 ; x^2+pх-q=0 ; p=1 ; q=a ; x1=4
теорема виета для приведенного квадратного уравнения
x1+x2 =-p = -1 ; 4+x2 = -1 ; x2 = -5
x1*x2 =q =a ; 4 *(-5) = -20
ОТВЕТ
x2 = -5
a= -20
2
x1=-5 ; x2 = 8
(x+5) (x-8) = x^2-8x+5x -40 = x^2-3x-40
5
то же самое ,что 2
3
а)
x^2/ (x+6) = 1/2 ;
ОДЗ x+6 = 0 ; x = -6 (- 6 исключаем из корней)
2x^2 = (x+6) ;
2x^2 - x- 6 =0;
D = (-1)^2 - 4*2(-6) =1+48=49 ; √D = √49 = -/+7
x1 = (1 -7 )/ (2*2)=-6/4 =-3/2 =- 1.5
x2 = (1 +7 )/ (2*2)=8/4 =2
ОТВЕТ -1.5 ; 2
б)
(x^2-x) / (x+3) = 12 / (x+3)
ОДЗ x+3 = 0 ; x = -3 (- 3 исключаем из корней)
(x^2-x) = 12
x^2-x - 12 =0
D = (-1)^2 - 4 *1*(-12)=49 ; √D = √49 = -/+7
x1 = (1-7) / 2 = -6/2 = -3 не входит в ОДЗ
x2 = (1+7) / 2 = 8/2 = 4
ОТВЕТ 4
В решении.
Объяснение:
называется "выделение полного квадрата).
1) х² + 8х - 1 = 0
х² + 8х + 4² - 4² - 1 = 0
(х + 4)² - 17 = 0
(х + 4)² = 17
х + 4 = ±√17
х = ±√17 - 4;
2) 2х² - 5х - 7 = 0/2
↓
х² - 2,5х - 3,5 = 0
х² - 2,5х + 1,25² - 1,25² - 3,5 = 0
(х - 1,25)² - 5,0625 = 0
(х - 1,25)² = 5,0625
х - 1,25 = ±√5,0625
х - 1,25 = ±2,25
х = -2,25 + 1,25
х₁ = -1;
х = 2,25 + 1,25
х₂ = 3,5;
3) 4х² - 16х - 1 = 0/4
↓
х² - 4х - 0,25 = 0
х² - 4х + 2² - 2² - 0,25 = 0
(х - 2)² - 4,25 = 0
(х - 2)² = 4,25
х - 2 = ±√4,25
х - 2 = ±√(0,25*17)
х - 2 = ±0,5√17
х = ±0,5√17 + 2;
4) 5х²/4 - 3х/7 - 3 = 0/5/4
х² - 12х/35 + (6/35)² - (6/35)² - 2,4 = 0
(х - 6/35)² - 2904/1225 = 0
(х - 6/35)² = 2904/1225
х - 6/35 = ±√(2904/1225)
х - 6/35 = ±√((16*186)/1225)
х - 6/35 = (±4√186)/35
х = (±4√186)/35 + 6/35.
Проверка путём подстановки вычисленных значений х в уравнения показала, что данные решения удовлетворяют данным уравнениям.