Объяснение:
Биквадратным называется уравнение вида ax ⁴+ bx ² + c =0 , где a <> 0 .
Биквадратное уравнение решается методом введения новой переменной: положив x ² = y , прийдем к квадратному уравнению ay ² + by + c =0 .
Пример: Решить уравнение x ⁴ +4 x ² -21=0 .
представим : x ⁴ --> t² ( буква может быть любая) , а x ² --> t . получится так: t ² + 4t - 21 = 0
решаем дискриминант :
D = ( 4)² - 4 × 1 × ( - 21 ) = 16 + 84 = 100 ( квадратный корень из 100 будет 10 )
теперь найдём корн уравнения:
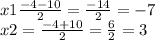
кони уравнения: x1 = -7 , a y = 3
Вернёмся к записи t²
t ² = ( подставляем сюда корни полученные ) - 7
- 7 --> не может быть отрицательный квадратный корень , значит корня нет
t ² = 3 ( здесь положительное число, значит будет 2 корня , а именно:
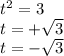
ответ би квадратного уравнения таков :
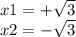
ответ: Уравнение эллипса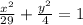 ; оси симметрии данного эллипса являются осями координат(или ось Ох и Оу); ε =5/√(29)
; оси симметрии данного эллипса являются осями координат(или ось Ох и Оу); ε =5/√(29)
Объяснение:
Дан эллипс: F₁ =(-5;0); F₂ =(5;0) и B₁=(0;-2); B₂=(0;2). Напишите уравнение эллипса, найти оси и эксцентриситет
фокусное расстояние эллипса с = 5 (от точки F до точки О)
малая полуось b = 2
большая полуось а находится из соотношения
а² = b² + c²
a² = 2² + 5² = 4 + 25 = 29
уравнение эллипса:
- каноническое уравнение эллипса
Оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии.
Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .
ε = с/ a = 5/√(29)