(см. объяснение)
Объяснение:
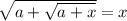
Если я правильно понял, то нужно решить уравнение при каждом значении параметра.
Возведем обе части уравнения в квадрат на условии, что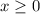 
.
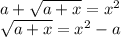
Возведем обе части уравнения в квадрат, добавив условие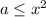 
.
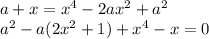
Решаем через дискриминант:
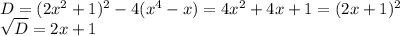
Найдем корни:
Итого исходному уравнению равносильно:
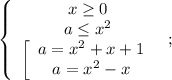
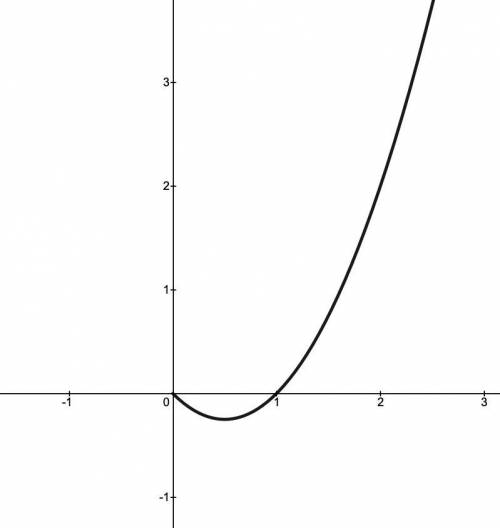
Строим все в координатах (x; a):
(см. прикрепленный файл)
Итого:
При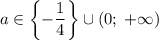
исходное уравнение имеет единственное решение.При ![a\in\left(-\dfrac{1}{4};\;0\right]](/tpl/images/2008/8379/66efc.png)
исходное уравнение имеет ровно два различных решения.При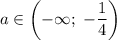 
исходное уравнение не имеет решений.Задание выполнено!
-10 108 10-9,5 97,75 10-9 88 10-8,5 78,75 10-8 70 10-7,5 61,75 10-7 54 10-6,5 46,75 10-6 40 10-5,5 33,75 10-5 28 10-4,5 22,75 10-4 18 10-3,5 13,75 10-3 10 10-2,5 6,75 10-2 4 10-1,5 1,75 10-1 0 10-0,5 -1,25 100 -2 100,5 -2,25 101 -2 101,5 -1,25 102 0 102,5 1,75 103 4 103,5 6,75 104 10 104,5 13,75 105 18 105,5 22,75 106 28 106,5 33,75 107 40 107,5 46,75 108 54 108,5 61,75 109 70 109,5 78,75 1010 88 10