1.Бригада маляров красит забор длиной 300 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 20 метров забора. Определите, сколько дней бригада маляров красила весь забор.
2. Грузовик перевозит партию щебня массой 160 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 3 тонны щебня. Определите, сколько тонн щебня было перевезено за восьмой день, если вся работа была выполнена за 16 дней.
3. В лесу живут белки, каждая из которых, придя на опушку, съедает 12 орехов. В первый день на опушку пришли 8?белок. В каждый следующий на опушку приходило на три белки больше. Сколько орехов съели белки за 21 дней?
4. Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 1 каплю, а в каждый следующий день?— на 2 капли больше, чем в предыдущий. Приняв в день 21 каплю, он ещё 3 дня пьёт по 21 капели лекарства, а потом ежедневно уменьшает приём на 2 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
5. В первом ряду кинозала 20 места, а в каждом следующем на 4 больше, чем в предыдущем. Сколько мест в десятом ряду?

👇

Увидеть ответ

Открыть все ответы

Ответ:

Помидоркин001

14.06.2020

1. Решим первое неравенство этой системы:

5 - 5x 11

-5x 11 - 5

-5x 6

$x < -\dfrac{6}{5}$

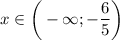
ответ: $x \in \bigg(-\infty; -\dfrac{6}{5} \bigg)$

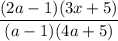2. Дробь $\dfrac{(2a-1)(3x+5)}{(a-1)(4a+5)}$ существует, если

$(a-1)(4a+5) \neq 0\\ \\\left[\begin{array}{ccc}a-1\neq0 \ \\4a+5\neq0 \\ \end{array}\right \ \ \ \ \ \ \ \left[\begin{array}{ccc}a\neq1 \ \ \ \\ a\neq -\dfrac{5}{4} \\ \end{array}\right$

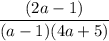Перед тем как выражать , нужно рассмотреть случаи, когда дробь $\dfrac{(2a-1)}{(a-1)(4a+5)}$ положительная, а когда отрицательная:

Если такая дробь положительная, то при нахождении переменной

знак неравенства меняться не будет (так как делим (умножаем) на положительное число):

$\dfrac{2a-1}{(a-1)(4a+5)} 0$

Решим неравенство методом интервалов.

а) ОДЗ: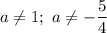 $a\neq 1; \ a\neq -\dfrac{5}{4}$

б) Нуль неравенства: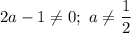 $2a-1 \neq 0; \ a \neq \dfrac{1}{2}$

в) Решением данного неравенства будет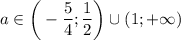 $a \in \bigg(-\dfrac{5}{4}; \dfrac{1}{2} \bigg) \cup (1; +\infty )$ .

При таких значениях параметра знак неравенства меняться не будет:

$\dfrac{(2a-1)(3x+5)}{(a-1)(4a+5)} 1 \ \ \ \ \bigg| : \dfrac{2a-1}{(a-1)(4a+5)}$

$3x+5 \dfrac{(a-1)(4a+5)}{2a-1}$

$3x \dfrac{(a-1)(4a+5)}{2a-1} - 5$

$3x \dfrac{4a^{2} + 5a - 4a - 5 - 5(2a-1)}{2a-1}$

$3x \dfrac{4a^{2} + a - 5 - 10a + 4}{2a - 1}$

$3x \dfrac{4a^{2} - 9a}{2a-1} \ \ \ \ \ \ | : 3$

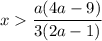
$x \dfrac{a(4a-9)}{3(2a - 1)}$

Если такая дробь отрицательная, то при нахождении переменной

знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):

$\dfrac{2a-1}{(a-1)(4a+5)} < 0$

Решим неравенство методом интервалов. Решением данного неравенства будет $a \in \bigg(-\infty; -\dfrac{5}{4}; \bigg) \cup \bigg(\dfrac{1}{2} ; 1 \bigg)$ .

При таких значениях параметра знак неравенства изменится:

$\dfrac{(2a-1)(3x+5)}{(a-1)(4a+5)} 1 \ \ \ \ \bigg| : \dfrac{2a-1}{(a-1)(4a+5)}$

$3x+5 < \dfrac{(a-1)(4a+5)}{2a-1}$

$x < \dfrac{a(4a-9)}{3(2a - 1)}$

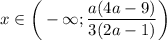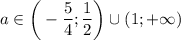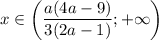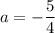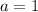ответ: если $a \in \bigg(-\infty; -\dfrac{5}{4}; \bigg) \cup \bigg(\dfrac{1}{2} ; 1 \bigg)$ , то $x \in \bigg (-\infty; \dfrac{a(4a-9)}{3(2a - 1)} \bigg)$ ; если $a \in \bigg(-\dfrac{5}{4}; \dfrac{1}{2} \bigg) \cup (1; +\infty )$ , то $x \in \bigg (\dfrac{a(4a-9)}{3(2a - 1)}; + \infty \bigg)$ ; если $a = -\dfrac{5}{4}$ и a = 1 , то неравенство не имеет решений.

3. Данная система неравенств решается в зависимости от значений параметра , поэтому:

1) Рассмотрим случай, когда решение неравенств пересекается:

Если $\dfrac{a(4a-9)}{3(2a - 1)} < -\dfrac{6}{5}$ , то есть $a \in \bigg(-\infty; -\dfrac{3}{4} \bigg) \cup \bigg(\dfrac{1}{2}; \dfrac{6}{5}\bigg)$ , то в объединении с $a \in \bigg(-\dfrac{5}{4}; \dfrac{1}{2} \bigg) \cup (1; +\infty )$ получаем $a \in \bigg(-\dfrac{5}{4}; - \dfrac{3}{4}\bigg) \cup \bigg(1; \dfrac{6}{5} \bigg)$ $x < \dfrac{a(4a-9)}{3(2a - 1)}$ при $a \in \bigg(-\infty; -\dfrac{5}{4}; \bigg) \cup \bigg(\dfrac{1}{2} ; 1 \bigg)$ Если $\dfrac{a(4a-9)}{3(2a - 1)} -\dfrac{6}{5}$ , то есть $a \in \bigg(-\dfrac{3}{4}; \dfrac{1}{2} \bigg)\cup \bigg(\dfrac{6}{5}; + \infty \bigg)$ , то в объединении с $a \in \bigg(-\infty; -\dfrac{5}{4}; \bigg) \cup \bigg(\dfrac{1}{2} ; 1 \bigg)$ получаем, что таких

не существует, то есть такого варианта эта система не имеет.

2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):

Оставшийся промежуток является решением этого варианта: $a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}$

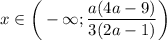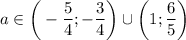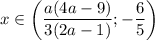ответ: если $a \in \bigg(-\infty; -\dfrac{5}{4}; \bigg) \cup \bigg(\dfrac{1}{2} ; 1 \bigg)$ , то $x \in \bigg (-\infty; \dfrac{a(4a-9)}{3(2a - 1)} \bigg)$ ; если $a \in \bigg(-\dfrac{5}{4}; - \dfrac{3}{4}\bigg) \cup \bigg(1; \dfrac{6}{5} \bigg)$ , то $x \in \bigg (\dfrac{a(4a-9)}{3(2a - 1)}; -\dfrac{6}{5} \bigg)$ ; если $a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}$ , то система не имеет решений.

4,6(71 оценок)

Ответ:

jelenazeile

14.06.2020

1) Иррациональные - это числа, которые нельзя выразить дробью a/b с целыми числителем и знаменателем.
2) Десятичные приближения по недостатку и по избытку - это десятичные дроби, между которыми заключено иррациональное число. Возьмём, например, √3~1,732. Его приближением до сотых долей по недостатку будет 1,73, а по избытку 1,74.
3) Классическое доказательство. Если √2 рационально, то его можно выразить несократимой дробью √2=a/b. Возведем все в квадрат. 2=a^2/b^2. То есть 2b^2=a^2. Теперь рассуждаем. Слева чётное число, значит a тоже чётное. Но чётный квадрат всегда делится на 4. Значит, b^2 тоже чётный. Но тогда а и b оба четные и дробь a/b можно сократить. Но мы условились, что дробь несократима. Противоречие. Значит, число √2 нельзя выразить дробью, то есть оно иррациональное.
4) Действительные - это все числа, и рациональные и иррациональные.
5) Действительные числа можно представить в виде точек на координатной прямой, причём это все точки на прямой.
6) Натуральные N, целые Z, рациональные Q, действительные R. Круги Эйлера нарисовать не могу, но могу объяснить. Действительные - самый большой круг, рациональные внутри, целые внутри рац-ных, натуральные внутри целых.

4,4(62 оценок)

Это интересно:

Стиль-и-уход-за-собой

25.09.2020

Как выглядеть великолепно голым: советы от профессионалов...

Стиль-и-уход-за-собой

11.09.2021

Как распутать парик: лучшие советы от профессионалов...

Кулинария-и-гостеприимство

07.04.2023

Отварная кукуруза в початках: легко и быстро...

Питомцы-и-животные