12см и 16 см
Объяснение:
1) Пусть одна сторона прямоугольника равна х см, тогда вторая - (х+4) см. Так как в прямоугольнике все углы прямые, найдём диагональ прямоугольника по теореме Пифагора:
х²+(х+4)²=20²
2х²+8х-384=0
х²+4х-192=0
D = 4²-4*(-192)=16+768=784=28²
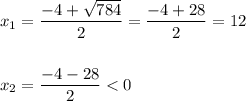
т.к. сторона не может быть меньше нуля, то меньшая сторона прямоугольника равняется 12см, большая: 12+4=16см
2) Если меньшую сторону обозначить через х см, а большую через у см, то получим следующие уравнения:
у-х=4 (одна сторона на 4 см больше от другой)х²+у²=20² (находим диагональ по т.Пифагора)Система уравнений, которая соответствует условию задачи:
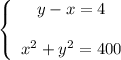

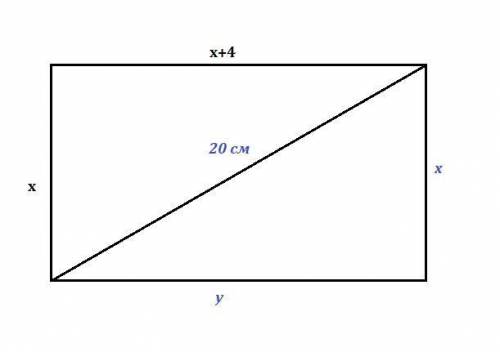
Объяснение:
Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.
Если плюс - скобки раскрываем, не меняя знака.