
1. а) 2x – 3(y – 1) + 2 = 0; 2x -3y +5=0 ;
Чтобы система
а₁х+b₁y+c₁=0
a₂x+b₂y+c₂=0
имела бесконечное множество решений, надо, чтобы прямые сливались, т.е. а₁/а₂=b₁/b₂=c₁/c₂, в вашем случае
2/4=-3/(-6)=5/(10), т.е. коэффициенты были пропорциональны, например, это второе уравнение 4х-6у+10=0
б) система не имеет решений, когда выполняется условие
а₁/а₂=b₁/b₂≠c₁/c₂, т.е. 2/4=-3/(-6)≠5/15
т.е. второе уравнение 4х-6у+15=0;
4х-6у+10=0
4х-6у+15=0
2. По рисунку вижу две прямые, у=0.5х+2 и у=-2х+7, и система, соответственно
у=0.5х+2
у=-2х+7, решением которой является точка (2;3), это по графикам линейных функций видно. Проверим?) подставим х=2; у=3 в оба уравнения, получим
3=0.5*2+2
3=-2*2+7, все верно. Уравнения прямых можно было не писать, я глянул на их угловые коэффициенты , и составил уравнения прямых, проходящих через две точки, получил у=0.5х+2 и у=-2х+7; но еще раз подчеркиваю, это только для того, чтобы Вас убедить, что решение на рисунке совпадает с точкой пересечения.
ответ х=2; у=3.
3. Чтобы решить систему, упростим ее предварительно, построим прямые и найдем решение. упростим первое уравнение.
3х+3у-2х=3+2у; у=-х+3; упростим второе уравнение.
-2у-4х=-3х-5; 2у=-х+5; Невооруженным глазом видим решение. Это точка (1;2), проверим графически. Строим каждую прямую, предварительно выбрав по две точки, находим точку пересечения, это и будет ответ. Далее - во вложении.

Доказать тождество:
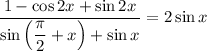
1. Определим область допустимых значений.
1.1. Выражение слева имеет смысл, если его знаменатель не равен нулю:
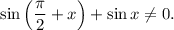
1.2. Используя формулу приведения 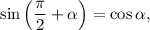 получаем:
получаем:
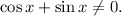
1.3. Умножим обе части на 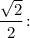
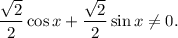
1.4. Поскольку 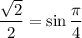 и
и 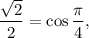 то получаем:
то получаем:
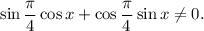
1.5. Используя формулу синуса суммы 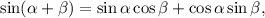 получаем:
получаем:
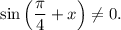
1.6. Так как 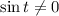 для
для 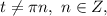 то:
то:
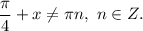
1.7. Перенесём 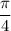 в правую часть, изменив знак на противоположный:
в правую часть, изменив знак на противоположный:
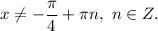
2. Докажем данное тождество, работая с левой частью равенства.
2.1. Преобразуем данное выражение, применив формулу косинуса двойного угла 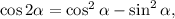 синуса двойного угла
синуса двойного угла 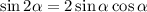 и формулу приведения
и формулу приведения 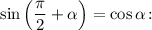
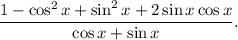
2.2. Замечаем в числителе следствие из основного тригонометрического тождества 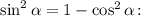
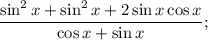
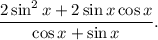
2.3. Вынесем в числителе общий множитель 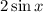 за скобки:
за скобки:
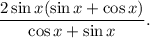
2.4. Сокращаем дробь на 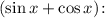
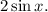
Тождество доказано.
ответ: 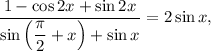 если
если 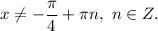
Пометка. Пункт под нахождением области допустимых значений не является обязательным при доказательстве тождества.
ответ во вложении
Объяснение:
Хорошего дня