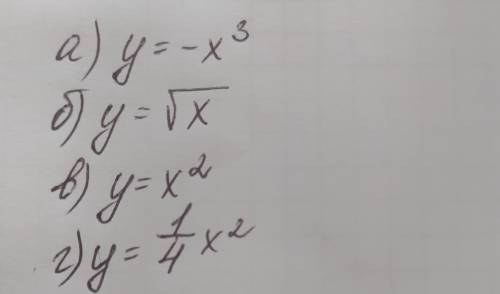
972 или 871
Объяснение:
пусть
x записано в виде abc, то есть
x=100a+10b+c
(а,b,c -натуральные от 1 до 9 или 0)
тогда по условию
100a+10b+c -( 100c+10b+a)=693
a+b+c=18
из первого получим
99a-99c=693
или
a-c=7
так как a и с могут принимать только целые неотрицательные значения от 0 до 9
то мы получаем следующие пары
а1=9 с1=2
а2=8 с2=1
а3=7 с3=0
теперь вспоминаем про второе условие
а+b+c=18
b=18-a-c
третий вариант не подходит, так как
b3=11
поэтому остаются следующие
а1=9 b1=7 с1=2
а2=8 b1=9 с2=1
откуда наше число
x1=972
или х2=891
1.
1) По условию ВМ=MD=14 см , где ВМ - высота параллелограмма АВCD.
2) AM+MD=AD
8см + 14см = 22см - длина стороны AD.
3) S = AD · ВМ - площадь параллелограмма АВCD.
22см · 14см = 308 см²
ответ: 308 см²
2.
Дано:
S = 12см²
ВК⊥AD
ВК = 2см
BM⊥DC
ВМ =3 см.
P=?
Решение.
1) S = AD · ВК - площадь параллелограмма.
AD = S : ВК
AD = 12 : 2 = 6 см - одна сторона параллелограмма.
2) S = DC · ВM - площадь параллелограмма.
DC = S : ВM
DC = 12 : 3 = 4 см - вторая сторона параллелограмма.
3) Р = 2· (AD+DС) - периметр параллелограмма.
Р = 2 · (6 + 4) = 20 см
ответ: 20 см.
3.
Дано:
Ромб QRMN
∠QRM = 60°
QD⊥RM
RD = 6
S=?
Решение.
1) ΔQRD - прямоугольный треугольник.
∠RQD = 90°- 60° = 30°
2) Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
RD =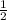 QR => QR = 2RD
QR => QR = 2RD
QR = 2 · 6 = 12см
QR=RM=MN=NQ - как стороны ромба.
3) По теореме Пифагора в прямоугольном треугольнике
RD²+DQ²=QR² => DQ²=QR² - RD²
DQ²=12² - 6²=144-36=108
DQ = √108 = 6√3 см - высота ромба
4) S = RM · DQ - площадь ромба
S = 12 · 6√3 = 72√3 ≈ 125
ответ: 72√3 см² или 125 см²