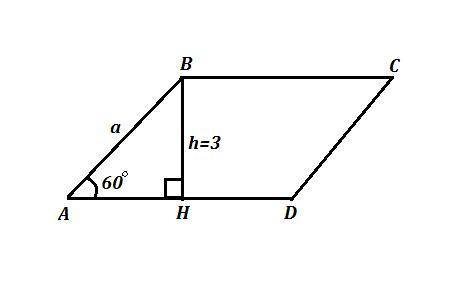
Высота ромба равна h=BH=3 , h ⊥ a или BH⊥AD .
Обозначим сторону ромба через а , острый угол - через х° .
Тогда тупой угол равен 2х° . Так как сумма углов, прилежащих к одной и той же стороне ромба, равна 180°, то х°+2х°=180° , 3х°=180° ,
х°=60° - острый угол
Рассмотрим ΔАВН , ∠АНВ=90° , а=h/sinx° ,
АВ=BH/sin60°=3/(√3/2)=2√3 .
Площадь ромба равна 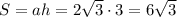 .
.
Или 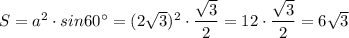 .
.
для меня это самое понятное... надеюсь
Объяснение:
Предположим, что нам нужно составить квадратное уравнение, корнями которого были бы числа x1 и x2. Очевидно, что в качестве искомого уравнения можно выбрать уравнение
a(х — x1)(х — x2) = 0, (1)
где а — любое отличное от нуля действительное число. С другой стороны, каждое квадратное уравнение с корнями x1 и x2 можно записать в виде (1).
Таким образом, формула (1) полностью решает поставленную выше задачу. Из всех квадратных уравнений корни x1 и x2 имеют уравнения вида (1) и только, они.
Пример. Составить квадратное уравнение, корни которого равны 1 и — 2.
ответ. Корни 1 и —2 имеют все квадратные уравнения вида
а(х — 1)(х + 2) = 0,
или
ах2 + ах — 2а = 0,
где а — любое отличное от нуля действительное число. Например, при а = 1 получается уравнение
х2 + х — 2 = 0.
Объяснение:
1) при х≥0 IxI=x
y=x²-4|x|-x=y=x²-4x-x=x²-5x
y=x²-5x графиком этой функции является парабола у которой
ветви направлены вверх так как коэффициент при х² равен 1 и 1≥0
абсцисса вершина параболы х₀=-b/2a=-(-5)/2=2,5
ордината вершины параболы у₀=у(х₀)=(2,5)²-5*2,5=-6,25
найдем абсциссы точек пересечения с ОХ
y=x²-5x =x(х-5) =0 х₁=0 ;x₂=5
2) при х<0 IxI=-x
y=x²-4|x|-x=y=x²+4x-x=x²+3x
y=x²+3x графиком этой функции является парабола у которой
ветви направлены вверх так как коэффициент при х² равен 1 и 1≥0
абсцисса вершины параболы х₀=-b/2a=-3/2=-1,5
ордината вершины параболы у₀=у(х₀)=(-1,5)²+3(-1,5)=2,25-4,5=-2,25
найдем абсциссы точек пересечения с ОХ
y=x²+3x =x(х+3) =0 х₁=0 ;x₂=-3
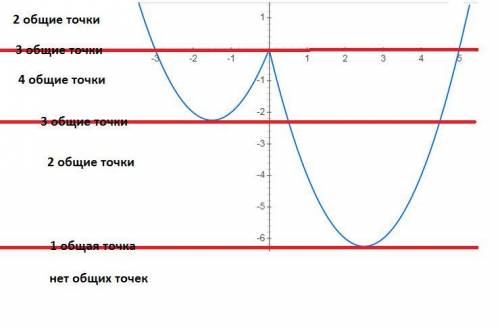
рассмотрим различные расположения прямой у=m
а) при m< -6,25 прямая y=m не имеет с графиком y=x^2-4|x|-x общих точек
б) при m=-6,25 прямая y=m имеет с графиком y=x^2-4|x|-x одну общую точку
в) при -6,25<m<-2,5 и 0<m прямая y=m имеет с графиком y=x^2-4|x|-x две общие точки
г) при m=-2,25 и m=0 прямая y=m имеет с графиком y=x^2-4|x|-x три общие точки
д) при -2,25<m<0 прямая y=m имеет с графиком y=x^2-4|x|-x четыре общие точки, эта область нам не подходит
таким образом прямая y=m имеет с графиком не менее одной, но не более трех общих точек
при m -6,25≤m≤-2,25 и m≥0
m∈[-6,25;-2,25]∪[0;+∞)
P=4a = 4*2=8
Объяснение:
острый угол = 180- тупой угол
H=√3 . пусть х острый угол , тогда тупой 2x ,
3x=180
x=60 гр , значит углы равны 60 и 120 градусов
Опустим высота получим прямоугольный треугольник
√3/sin60=a где "а" сторона ромба
a=2
P=4a = 4*2=8