Построим график функции у = 8 + 2x - x²
Для этого преобразуем её к виду
у = -(х² - 2х + 1) + 9
у = -(х - 1)² + 9
Видим, что парабола у = -х² сдвинута по оси абсцисс на 1 вправо и на 9 вверх. То есть её вершина находится в точке с координатами (1; 9).
Найдём координаты точек пересечения параболы с осью ординат.
При х = 0 у = 8
И координаты точек пересечения параболы с осью абсцисс
у = 0
- х² + 2х + 8 = 0
D = 2² - 4 · (-1) · 8 = 36
√D = 6
х₁ = -0,5(-2 - 6) = 4
х₂ = -0,5(-2 + 6) = -2
Итак мы получили ещё две точки параболы (4; 0) и (-2; 0).
Строим параболу (веточки её опущены вниз).
Смотри прикреплённый рисунок.
1) по графику видим, что функция убывает на интервале х ∈ [1; +∞)
2) множество решений неравенства 8 + 2x - x^2 ≤ 0 есть объединение двух интервалов х∈ (-∞; -2] ∪ [4; +∞)
Если в уравнении рассматриваются частные случаи sinx=0 и cosx=0, то пользуются более простыми формулами, и пользуются периодом П, так как нули синуса и косинуса повторяются через период, равный П, хотя в общем случае наименьший положительный период для этих функций равен 2П.
sinx=0, x=πn
cosx=0, x=π/2+πn
В общем случае sinx=a, x=(-1)^n*arcsina+πn и в случае sinx=0 можно было бы записать
х=(-1)^n*arcsin0+πn=(-1)^n*0+πn=πn.
Если решаем ур-ие sinx=1, то x=π/2+2πn - частный случай, а в общем случае писали бы х=(-1)^n*arcsin1+πn=(-1)^n*π/2+πn - ,более сложный вид, но правольная запись.
sinx=-1 x=-π/2+2πn - частный случай
Если cosx=a,то х=±arccosa+2πn.Можно для ур-ия cosx=0 записать решение через общую формулу х=±arccos0+2πn=±π/2+2πn (это более сложная запись, но правильная)
cosx=1, x=2πn
cosx=-1, x=π+2πn
Для уравнений tgx=a, x=arctga+πn
ctgx=a, x=arcctga+πn
Итак, если использовать общие формулы, то период только для косинуса берём 2πn. а для остальных функций используем πn.
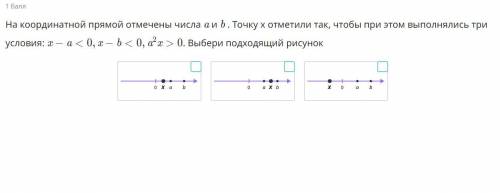
Первый рисунок
0Хab
Объяснение:
ответом является первый рисунок, т.к.
во-первых, на первом число Х расположено левее чисел a и b, т.е.
Х<a => X-a <0
X <b => X-b <0
во-вторых, число Х>0, a>0 => a²>0. Следовательно, a²X >0