Пусть дано некоторое число n. Число перед ним — n-1, число после него — n+1. Рассмотрим их разность:
Квадрат числа n больше произведения числа перед и после этого числа на единицу, что и требовалось доказать.
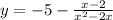
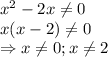
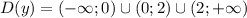
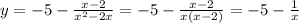
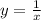, отображенную симметрично оси абсцисс и сдвинутую на 5 единиц вниз. Помним про то, что функция не определена в точках 0 и 2.
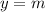представляет собой прямую, параллельную оси абсцисс, проходящую через точку (0; m). 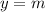не имеет общих точек с построенным графиком при 
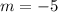(асимптота гиперболы по построению, так как сдвиг проводился на 5 единиц вниз) и при 
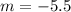(именно это значение принимала бы функция 
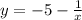в точке 2, но эта точка не принадлежит области ее определения).
Пусть х - целое число.
х - 1 - предыдущее
х + 1 - последующее
Найдем разность квадрата числа и произведения последующего и предыдущего:
x² - (x - 1)(x + 1) = x² - (x² - 1) = x² - x² + 1 =1