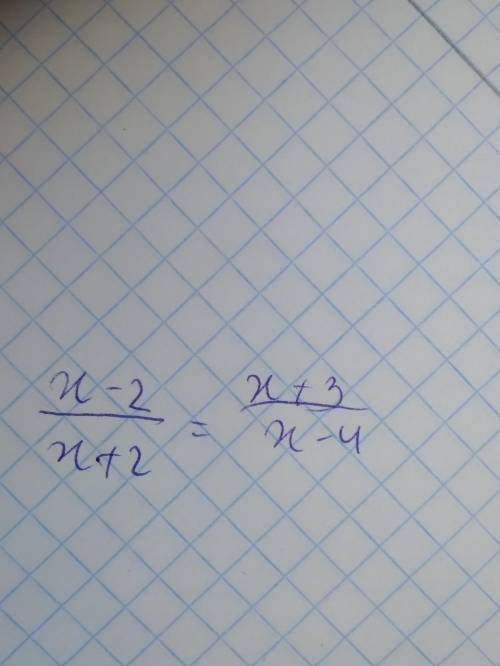
2/11
Объяснение:
ОДЗ: знаменатели ≠0.
х+2≠0 → х≠ -2 и х-4≠0 → х≠4
Это пропорция. Произведение крайних членов=произведению средних.
(х+2)(х+3)=(х-2)(х-4)
по правилу фонтанчика
х²+3х+2х+6=х²-4х-2х+8
3х+2х+6= -4х-2х+8
приводим подобные
5х+6= -6х+8
5х+6х= 8-6
11х=2
х=2/11
дискриминант тут не нужен, уравнение стало линейным!
В решении.
Объяснение:
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
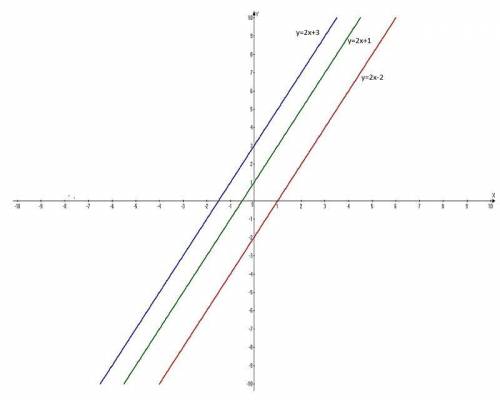
у = 2х + 1 у = 2х - 2 у = 2х + 3
Таблицы:
х -1 0 1 х -1 0 1 х -1 0 1
у -1 1 3 у -4 -2 0 у 1 3 5
Вывод по построению: графики функций, значения k которых равны (k=2), параллельны друг другу.
Рассмотрим уравнение 2^x +2x =1, сумма возрастающих функций есть возрастающая функция. Справа константа. Значит у данных графиков может быть только одна точка пересечения, что соответствует значению x = 0.
Если решать аналитически, то 2^x = 1-2x. Слева у нас функция >0, возрастает, справа функция убывающая, значит мы не можем рассматривать x, которые >= 1/2, а можем только x <=1/2
Тогда рассмотрим f(x) = 2^x+2x-1 = 0, Найдем f'(x) = 2^x*ln(2)+2, найдем f'(x) = 0, тогда 2^x*ln(2)+2 =0, откуда делаем вывод, что при любых иксах наша функция возрастает, тогда уравнение будет иметь не более одного корня, ведь слева 2^x+2x непрерывна и возрастает для всех значений икс, а справа константа, значит ответ х = 0
2/11
Объяснение:
(x-2)/(x+2)=(x+3)/(x-4)
(x-2)/(x+2) -(x+3)/(x-4)=0
((x-2)(x-4)-(x+3)(x+2))/((x+2)(x-4))=0
x+2≠0; x≠-2
x-4≠0; x≠4
x²-6x+8-x²-5x-6=0
-11x+2=0
11x=2
x=2/11