Функция задана уравнением y = x² – 4x - 5
Это парабола ,ветви вверх. Область определения :х-любое, множество значений функции [ -9; +∞) ;
а) Найдите вершину параболы
х₀=-в/2а, х₀=-(-4)/2= 2 , у₀=2²-4*2 -5= -9 , ( 2; -9).
Тогда наименьшее значение функции у=-9 ( при х=2)
Наибольшего значения нет ;
b) В какой точке график данной функции пересекает ось ОY.
Точки пересечения с оу ( х=0)
у= 0²- 4*0-5=-5, Точка (0; -5).
c) Найдите точки пересечения графика функции с осью ОХ.
Точки пересечения с осью ох( у=0)
x²- 4x-5=0 , Д=36 , х₁=(4+6)/2=5, х₂=(4-6)/2=-1. Точки (5;0) , ( -1;0).
d) Запишите уравнение оси симметрии графика данной функции :
х=2.
e) Постройте график функции.Смотри ниже
f) Найдите промежутки возрастания убывания функции
Функция убывает при х≤ 2 ,
функция возрастает при x≥2;
Промежутки знакопостоянства функции :
+ . - .+
______(-1)_______(5)_______
у>0 при х <-1 и x>5
у<0 при -1 <х< 5 ;
Доп. точки у= x²- 4x-5:
х: -2 1 6
у: 7 -8 7

Находим частные производные:
∂z/∂x=6y-18x+4
∂z/∂y=6x-18y+4
Находим стационарные точки:
{∂z/∂x=0 ⇒ 6y-18x+4=0
{∂z/∂y=0 ⇒ 6x-18y+4 =0
Решаем систему:
{ 6y-18x+4=0 ( умножаем на 3)
{6x-18y+4 =0
{ 18y-54x+12=0
{6x-18y+4 =0
cкладываем
-48х+16=0
х=1/3
y=1/3
Стационарная точка (1/3;1/3) принадлежит области ( см. рис)
Находим вторые частные производные
∂²z/∂x²=-18
∂²z/∂y²=-18
∂²z/∂x∂y=6
A=-18; B=-18: C =6
Δ=AB-C²=(-18)·(-18) -6²>0
A < 0
(1/3;1/3) - точка максимума
z(1/3;1/3)=6·(1/3)·(1/3)-9·(1/3)²-9·(1/3)²+4·(1/3)+4·(1/3)=(2/3)-1-1+(8/3)=4/3 - наибольшее значение функции
На границе
При x=0
z=-9y²+4y
Квадратичная функция при 0 ≤y ≤2
z`=-18y+4
z`=0
y=4/18=2/9 - точка максимума
z(2/9)=-9·(2/9)²+4·(2/9)=(-4/9)+(8/9)=4/9 < 4/3
z(0)=0
z(2)=-9·2²+4·2=-28
При y=0
z=-9x²+4x
Квадратичная функция при 0 ≤x ≤1
z`=-18y+4
z`=0
y=4/18=2/9 - точка максимума
z(2/9)=-9·(2/9)²+4·(2/9)=(-4/9)+(8/9)=4/9 < 4/3
z(0)=0
z(1)=-9·1²+4·1=-5 > -28
При х=1
z=6y-9-9y²+4+4y, исследуем на [0;2], 0 ≤y≤2
z(y)=-9y²+10y-5 - квадратичная функция
z`=-18y+10
z`=0
-18y+10=0
y=10/18=5/9 - точка максимума
при y=5/9
z=-9·(5/9)²+10·(5/9)-5 =- (25/9)+(50/9) -5 =-20/9
Находим значения на концах
z(0)=-5
z(2)=-9·2²+10·2-5=-21 > -28
При y=2
z=12x-9x²-9·2²+4x+4·2, исследуем на [0;1], 0 ≤x≤1
z(y)=-9x²+16x-28 - квадратичная функция
z`=-18x+16
z`=0
-18x+16=0
x=16/18=8/9 - точка максимума
при x=8/9
z=-9·(8/9)²+16·(8/9)-28 =- (64/9)+(128/9) -28 >-28
Находим значения на концах
z(0)=-28
z(1)=-9·1²+16·1-28=-21 > -28
z(1/3;1/3)=4/3 - наибольшее значение функции в области
z(1;2) =-28 - наибольшее значение функции в области
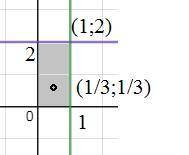
Объяснение:
у = 4х - 2
1) х= -2 → у=4*(-2)-2= -8-2= -10
2) у= -1 →
4х-2= -1
4х= -1+2
4х=1
х=1/4
3) 4 * 3 - 2 = 10 → 10 ≠ 40 → не проходит