По формуле:
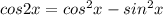
Зная это получаем:
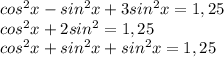
Известно что:
отсюда получаем:
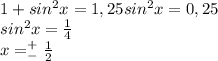
Получаем 2 уравнения:
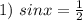это табличное значение синуса и получается 2 решения:
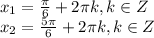
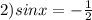аналогично получаем 2 решения:
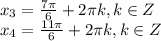
Теперь обратим внимание, что эти 4 решения можно записать в 2 решения в виде:
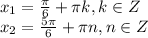
Теперь надо найти при каких значениях k и n решения лежат на отрезке ![[0; \frac{5\pi}{2}]](/tpl/images/0071/0603/9e0ce.png)
Для этого решаем 2 неравенства
1) 
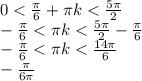
Так как к у нас принадлежит целым числам, то получается что к=0,1,2
2) Теперь ищем n, аналогично:
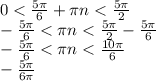
Поскольку n принадлежит целым числам, то получается что n=0,1
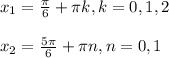
3) x² + 8х= -16 - 2x 4) х² + х - 2 = 2 - 2x
х²+8х+16+2х=0 х² + х - 2-2+2х=0
х²+10х+16=0 х²+3х-4=0
Д=в²-4ас Д=в²-4ас
Д=10²-4*1*16 Д=з²-4*1*(-4)
Д=36 Д=25
y=-1,2c
вгт