Положим, у Вас есть график у=f(х), если Вам надо построить график у=f(x+4), передвигаете вдоль оси ох на 4 единицы влево график функции у=f(х), если строите график у=f(x-4), то передвигаете на 4единицы вправо график у=f(х).
По Вашему рисунку 5, сначала строите график у=sinx, а затем переносите этот график на π/3 вправо, т.е. на две клетки тетрадной страницы и получаете график у=sin(x-π/3), т.к. отнимаем от аргумента π/3
Если бы пришлось к функции добавить 4 единицы, график подняли бы на 4единицы вверх, если отняли 4 единицы, то график опустили бы на 4 единицы вниз.
по первой картинке 4. Просто построили график у=cosx по точкам, а потом умножили на 1/2, т.е. сплюстнули в два раза график, он стал ниже в два раза, если бы был у=2cosx , то график стал бы выше в два раза.
Вот такие вот преобразования графика тригонометрической функции.
1. Здесь мы учитываем порядок, значит используем размещение. Первым моджет быть один из пяти предметов, вторым, один из четырех и т.д.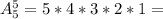
120
2. Здесь необходимо использовать сочетание, а не размещение, так как нам необходимо считать наборы отличающиеся только порядком элементов - одинаковыми (например: {1,2,3,4},{1,3,2,4}) . Сочетание же различает только те наборы у которых различается состав элементов.
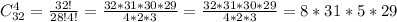= 35960
3. На первую позицию можно поставить одно из шести чисел, на вторую, одно из оставшихся пяти: 6*5 = 30
12 21 31 41 51 61
13 23 32 42 52 62
14 24 34 43 53 63
15 25 35 45 54 64
16 26 36 46 56 65
4. n = 45, w = 17, b = 45 - 17 = 28
После того, как потеряли два не белых шарика, осталось n = 43, w = 17, b = 26
Вероятность вытащить белый равна 17/43 (количество положительных исходов, ко всем исходам)
5. Всего возможных исходов(1 - орел, 0 - решка):
000
001
010
011
100
101
110
111
n = 8. (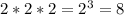
)
Положительных исходов: 011, 101, 110. m = 3 (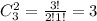
)
p = 3/8
Если же нам необходимо выпадение именно набора 110 (орел орел решка), тогда положительный исход один и вероятность будет 1/8
6. Всего исходов n = 1000000, положительных m = 1200+800 = 2000, p(m) = 2000/1000000 = 2/1000 = 0.002
7. Двухзначных чисел всего 90. Первое двузначное число 10, последнее 99. При делении на 13 даёт в остатке 5, число 18. Следующее 18+13 = 31, потом 44, 57, 70, 83, 96. Таких чисел 7.
Вероятность выбрать двухзначное число, которое будет давать остаток 5 при делении на 13 = 7/90 (число положительных исходов к числу всех исходов)
фото