ответ.
Раскроем скобки, соберём подобные члены и упростим выражение. Затем подставим значение переменной и вычислим значение выражения .
; 
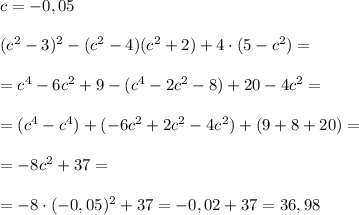
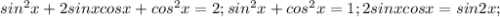
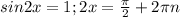, n∈Z;
, n∈Z;![[- \pi ; 2 \pi ]](/tpl/images/0759/4134/58ed4.png)
:
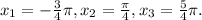
7
Объяснение:
Найти значение выражения: (у²-6у+9)/(у²-9) ∶ (10у-30)/(у²+3у) при у=70.
(у²-6у+9)/(у²-9) ∶ (10у-30)/(у²+3у)=
В числителе первой дроби развёрнут квадрат разности, свернуть, в знаменателе разность квадратов, развернуть.
В числителе второй дроби вынести 10 за скобки, в знаменателе вынести у за скобки:
=(у-3)²/[(у-3)(у+3)] : [10(у-3)]/[у(у+3)]=
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй, а знаменатель первой умножить на числитель второй.
=[(у-3)(у-3)у(у+3)] : [(у-3)(у+3)10(у-3)]=
сокращение (у-3) и (у-3) на (у-3) 2 раза, (у+3) и (у+3) на (у+3):
=у/10=70/10=7
(c²-3)²-(c²-4)(c²+2)+4(5-c²)=c⁴-6c²+9-c⁴+4c²-2c²+8+20-4c²=-8c²+37
c=-0.05
-8*(-0.05)²+37=-0.02+37=36.98
Объяснение: