Чтобы изобразить график линейной функции вида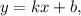 
где 
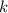и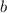 
— коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
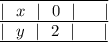
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение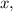 
подставляйте его в функцию и находите 
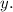(Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции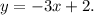 
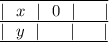
Строим таблицу для двух точек:
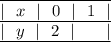
Пусть 
Тогда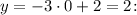 
Пусть 
Тогда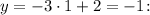 
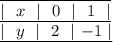
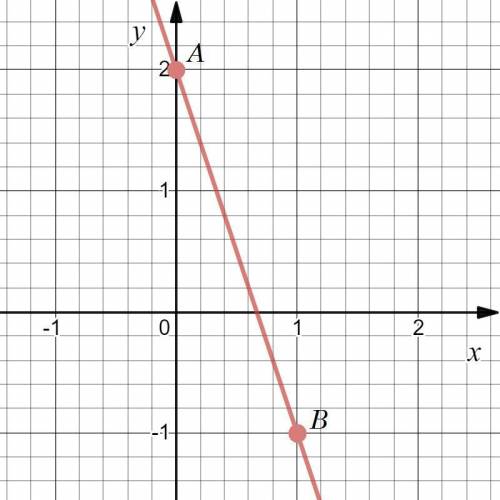
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точк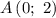и: 
и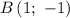 
— и проведем через них прямую (см. вложение). График линейной функции 
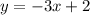построен.
Определим в каких четвертях располагаются углы 2, 4 и 6 радиан:
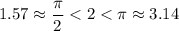
Угол в 2 радиана принадлежит 2 четверти.
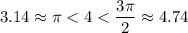
Угол в 4 радиана принадлежит 3 четверти.
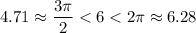
Угол в 6 радиан принадлежит 4 четверти.
Рассмотрим выражения:
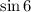- синус в 4 четверти принимает отрицательные значения
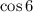- косинус в 4 четверти принимает положительные значения
Сразу отметим, что разность 
отрицательна, так как из отрицательного числа вычитается положительное
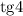- тангенс в 3 четверти принимает положительные значения
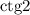- котангенс во 2 четверти принимает отрицательные значения
Итак, у нас есть 3 сомножителя знаки которых нам известны:
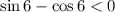
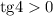
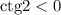
Произведение двух отрицательных и одного положительного числа положительное:
ответ: знак (+): выражение положительно
Смотрите: существует два правила...
1) Система из двух линейных уравнений не имеет решений, если прямые, получаемые при построении графиков данных уравнений, параллельны.
2) Система из двух линейных уравнений имеет бесконечно много решений, если прямые полностью совпадают.
А вот уже другой вопрос, как сделать так, чтобы они были параллельны, совпадали или пересекались?
Для этого существует тоже несколько условий. Но, чтобы о них сказать, я вам напомню, что любое линейное уравнение (которое приведено у вас в системе) имеет вид ах+bу+с=0. То есть то число, которое стоит перед буквой "х" называют коэффициентом a. То, что стоит перед буквой "у" называют коэффициентом b. А то число, которое стоит свободно, без букв, называют свободным коэффициентом с.
Итак, о правилах:
1) Если в двух линейных уравнениях, имеющих вид a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0 соблюдается a₁=a₂, b₁=b₂ и c₁=c₂, то прямые совпадают.
2) Если в двух тех же самых уравнениях соблюдается a₁=a₂, b₁=b₂, но c₁≠c₂, то прямые параллельны.
3) Если в двух тех же самых уравнениях различается хоть одна пара из коэффициентов a или b, то прямые пересекаются.
Итак, рассмотрим первый случай, под цифрой 1.
У уравнений этих прямых (они имеют общий вид ax+by+с=0) одинаковые коэффициенты a и b. Значит, мы можем сделать так, чтобы они не имели решений. Как? Верно, мы должны сделать так, чтобы коэффициенты c (свободное число) были разными. То есть можно вставить вместо а любое число, кроме 5. Например:
Рассмотрим случай под цифрой 2.
Мы видим, что коэффициенты a и b отличаются. Значит, быть может, нам нельзя сделать уравнения одинаковыми, чтобы прямые совпадали? Нет, мы можем это сделать, так как, если посмотреть на второе уравнение системы, то заметим, что его можно разделить на 3 (то есть все коэффициенты уменьшить в 3 раза). Делаем, получаем:
Теперь мы видим, что a₁=a₂ и c₁=c₂. Чтобы прямые совпадали, делаем так, что b₁=b₂. Тогда система имеет бесконечно много решений. Обратите внимаение, что в первом уравнении перед буковкой а стоит минус. Поэтому, чтобы получить 4у, мы ставим не b=4, а b=-4, так как минус на минус даст плюс.