1) Найдем нулю нашей функции. Для чего разложим на множители формулу, которой она задана, с введения новых вс членов.
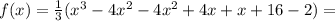
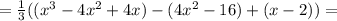
![=\frac{1}{3}[x(x-2)^{2}-4(x-2)(x+2)+(x-2)]=](/tpl/images/0065/5986/78255.png)
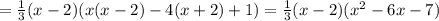
Из 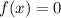 следует:
следует:
а) 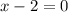 , отсюда
, отсюда 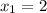 - нуль функции
- нуль функции
б) 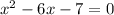 ,
, 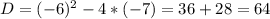 , отсюда
, отсюда
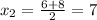 ,
, 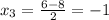 - нули функции
- нули функции
Итак, функция 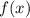 обращается в нуль в точках
обращается в нуль в точках 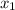 ,
, 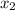 и
и 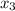
2) Найдем возможные точки экстремума нашей функции. Для чего найдем производную функции 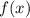 :
:
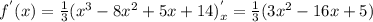 -----(1)
-----(1)
Разложим квадратный трехчлен, стоящий в правой части (1), на целые множители. Для чего найдем дискриминант этого квадратного трехчлена:
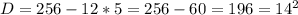 , отсюда найдем корни:
, отсюда найдем корни:
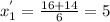
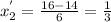 ---------(2)
---------(2)
Тогда с (2) выражение (1) примет вид метода интервалов найдем промежутки, на которых производная функции 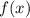 принимает положительные и отрицательные значения:
принимает положительные и отрицательные значения:
а) 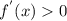 при x принадлежащем объединению промежутков
при x принадлежащем объединению промежутков
(-бесконечности; 1/3)U(5; +бесконечности )
б) 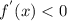 при x принадлежащем промежутку (1/3; 5)
при x принадлежащем промежутку (1/3; 5)
Известно, что промежутки, на которых производная функции положительна, являются промежутками возрастания функции!
На промежутках, где 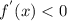 , функция убывает!
, функция убывает!
Поскольку при переходе через точку x=1/3 производная меняет знак с плюса на минус, то эта точка - точка максимума
Поскольку при переходе через точку x=5 производная меняет знак с минуса на плюс, то эта точка - точка минимума. Итак,

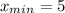
Начнем с того, что все простые числа, кроме числа 2, - нечетные.
Если среди чисел p и q нет числа 2, то они оба нечетные. Тогда, сумма двух нечетных чисел даст четное число, причем это четное число будет больше 2, так как наименьшие последовательные нечетные простые числа - это числа 3 и 5. Такое четное число не может быть простым. Значит, этот вариант не подходит.
Рассмотрим вариант, когда одно из двух рассматриваемых чисел равно 2. По условию, рассматриваются последовательные простые числа, значит другое число равно 3. Сумма этих чисел дает также простое число 5. Значит, сумма двух последовательных простых чисел может быть простым числом.
ответ: да, может