Question

Вычислить комплексное число в виде тригонометрической записи
(1+i)⁹×(1-i)¹⁵

Answer 1

$(1+i)^9\cdot (1-i)^{15}$

Рассмотрим число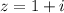 $z=1+i$. Запишем его в тригонометрической форме:

$|z|=\sqrt{1^2+1^2} =\sqrt{2}$

$\arg z=\mathrm{arctg}\,\dfrac{1}{1} =\dfrac{\pi }{4}$

$\Rightarrow 1+i=\sqrt{2} \left(\cos \dfrac{\pi }{4} +i\sin\dfrac{\pi }{4}\right)$

Аналогично, преобразуем число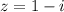 $z=1-i$:

$|z|=\sqrt{1^2+(-1)^2} =\sqrt{2}$

$\arg z=\mathrm{arctg}\,\dfrac{-1}{1} =-\dfrac{\pi }{4}$

$\Rightarrow 1-i=\sqrt{2} \left(\cos\left(- \dfrac{\pi }{4}\right) +i\sin\left(- \dfrac{\pi }{4}\right)\right)$

Для возведения комплексного числа в степень воспользуемся формулой Муавра:

$(\rho(\cos\varphi+i\sin\varphi))^n=\rho^n(\cos n\varphi+i\sin n\varphi)$

Получим:

$(1+i)^9=\left(\sqrt{2} \left(\cos \dfrac{\pi }{4} +i\sin\dfrac{\pi }{4}\right)\right)^9=(\sqrt{2})^9 \left(\cos \dfrac{9\pi }{4} +i\sin\dfrac{9\pi }{4}\right)$

$(1-i)^{15}=\left(\sqrt{2} \left(\cos\left(- \dfrac{\pi }{4}\right) +i\sin\left(- \dfrac{\pi }{4}\right)\right)\right)^{15}=$

$=(\sqrt{2})^{15} \left(\cos\left(-\dfrac{15\pi }{4}\right) +i\sin\left(- \dfrac{15\pi }{4}\right)\right)$

Далее, воспользуемся правилом умножения комплексных чисел в тригонометрической форме:

$\rho_1(\cos\varphi_1+i\sin\varphi_1)\cdot\rho_2(\cos\varphi_2+i\sin\varphi_2)=\rho_1\rho_2(\cos(\varphi_1+\varphi_2)+i\sin(\varphi_1+\varphi_2))$

Получим:

$(\sqrt{2})^9 \left(\cos \dfrac{9\pi }{4} +i\sin\dfrac{9\pi }{4}\right)\cdot(\sqrt{2})^{15} \left(\cos\left(-\dfrac{15\pi }{4}\right) +i\sin\left(- \dfrac{15\pi }{4}\right)\right)=$

$=(\sqrt{2})^{9+15} \left(\cos\left(\dfrac{9\pi }{4}-\dfrac{15\pi }{4}\right) +i\sin\left(\dfrac{9\pi }{4}- \dfrac{15\pi }{4}\right)\right)=$

$=(\sqrt{2})^{24} \left(\cos\left(-\dfrac{6\pi }{4}\right) +i\sin\left(- \dfrac{6\pi }{4}\right)\right)=2^{12} \left(\cos\left(-\dfrac{3\pi }{2}\right) +i\sin\left(- \dfrac{3\pi }{2}\right)\right)=$

$=4096 \left(\cos\left(2\pi -\dfrac{3\pi }{2}\right) +i\sin\left(2\pi - \dfrac{3\pi }{2}\right)\right)=\boxed{4096 \left(\cos\dfrac{\pi }{2}+i\sin\dfrac{\pi }{2}\right)}$

Получен ответ в тригонометрической форме записи. При необходимости его представить в алгебраической:

$4096 \left(\cos\dfrac{\pi }{2}+i\sin\dfrac{\pi }{2}\right)=4096(0+i\cdot1)=4096i$

Решение можно было несколько упростить, применив в начале формулу разности квадратов:

$(1+i)^9\cdot (1-i)^{15}=(1+i)^9\cdot (1-i)^9\cdot(1-i)^6=((1+i)(1-i))^9\cdot(1-i)^6=$

$=(1^2-i^2)^9\cdot(1-i)^6=(1+1)^9\cdot(1-i)^6=2^9\cdot(1-i)^6=$

$=2^9\cdot\left(\sqrt{2} \left( \cos\left(- \dfrac{\pi }{4}\right) +i\sin\left(- \dfrac{\pi }{4}\right)\right)\right)^6=$

$=2^9\cdot(\sqrt{2})^6 \left( \cos\left(- \dfrac{6\pi }{4}\right) +i\sin\left(- \dfrac{6\pi }{4}\right)\right)=$

$=2^{9+3} \left( \cos\left(2\pi - \dfrac{3\pi }{2}\right) +i\sin\left(2\pi - \dfrac{3\pi }{2}\right)\right)=\boxed{4096 \left( \cos\dfrac{\pi }{2} +i\sin\dfrac{\pi }{2}\right)}$