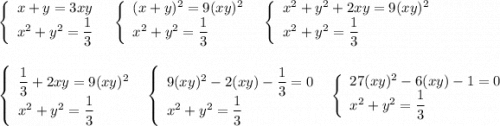
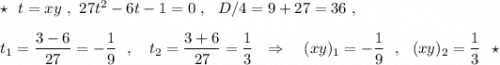
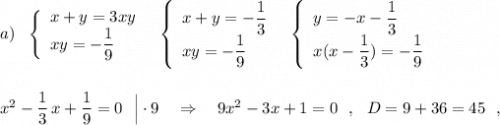
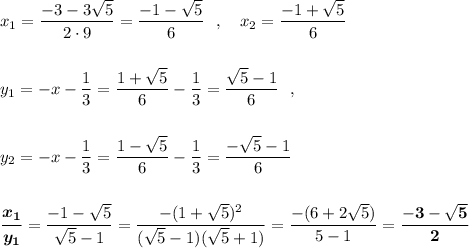
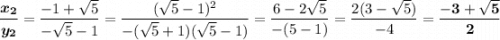

Так как D<0 , то действительных корней нет . Система не имеет решений .
ответ: 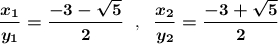 .
.
Все стороны квадрата равны. Допустим сторона квадра будет x.
Тогда площадь квадрата будет равна 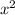 . По условию площадь увеличилась в 16 раз, то есть стала равна
. По условию площадь увеличилась в 16 раз, то есть стала равна 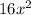 . Так как она увеличилась, следовательно увеличили саму сторону квадрата. Увеличили ее в 4 раза, так как новая площадь это
. Так как она увеличилась, следовательно увеличили саму сторону квадрата. Увеличили ее в 4 раза, так как новая площадь это 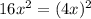 . Мы узнали, что сторона квадрата увеличилась в 4 раза, теперь узнаем во сколько раз увеличится периметр. Так как периметр квадрата без увеличение его сторон будет равен 4x, то при увеличении стороны в 4 раза он будет равен 4*4x=16x. То есть периметр увеличился в 4 раза.
. Мы узнали, что сторона квадрата увеличилась в 4 раза, теперь узнаем во сколько раз увеличится периметр. Так как периметр квадрата без увеличение его сторон будет равен 4x, то при увеличении стороны в 4 раза он будет равен 4*4x=16x. То есть периметр увеличился в 4 раза.
В решении.
Объяснение:
Решить неравенство:
1) 3(х + 4) + 2(3х - 2) > 5х - 3(2х + 4)
Раскрыть скобки:
3х+12+6х-4 > 5х-6х-12
Привести подобные члены:
9х+х > -12-8
10х > -20
х > -20/10
х > -2
x∈(-2; +∞) ответ а)
Неравенство строгое, скобки круглые.
2) 2х - 6 - 5(2 - х) <= 12 - 5(1 - x)
Раскрыть скобки:
2х-6-10+5х <= 12-5+5х
Привести подобные члены:
7х-5х <= 7+16
2х <= 23
x <= 23/2
x <= 11,5
х∈(-∞; 11,5] ответ б)
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда с круглыми скобками.
3) х + 2 < 5(2х + 8) + 13(4 - х) - 3(х - 2)
Раскрыть скобки:
х+2 < 10х+40+52-13х-3х+6
Привести подобные члены:
х+6х < 98-2
7х < 96
х < 96/7
x < 13 и 5/7
х∈(-∞; 13 и 5/7) ответ в)
Неравенство строгое, скобки круглые.
х/у=(-3+-sqrt(5))/2
Объяснение: