Сумма острых углов прямоугольного треугольника равна 90° .
Это следствие из теоремы о сумме внутренних углов треугольника . Так как сумма внутренних углов треугольника равна 180° , и в прямоугольном треугольнике есть прямой угол, равный 90° , то сумма остальных двух острых углов равна 180°-90°=90° .
Поэтому, чтобы найти острый угол прямоугольного треугольника , надо из 90° вычесть известное значение второго острого угла .
Все гири имеют различный вес, назовём их в порядке возрастания веса: g₁<g₂<g₃<g₄<g₅. Гири весят натуральное число грамм, поэтому минимальная разница между гирями 1г.
В решении я не буду использовать другие ед. измер., только граммы, поэтому, для упрощения записей, я не буду писать гр.
Пусть минимальный воможный вес для g₁ это x. Тогда: для g₂ - x+1; g₃ - x+2; g₄ - x+3; g₅ - x+4.
Самый минимальный суммарный вес для трёх гирь можно собрать из g₁ , g₂ , g₃ ; а самый максимальный для двух - g₄ , g₅.
Любые три гири весят больше, чем две другие, составим неравество и решим его.
g₁+g₂+g₃>g₄+g₅ ⇒ x+(x+1)+(x+2)>(x+3)+(x+4)
3x+3>2x+7; 3x-2x>7-3; x>4, 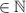 ⇒ x=5
⇒ x=5
Получаем, что минимальный суммарный вес для всех гирь 5+(5+1)+(5+3)+(5+4)+(5+5) = 5+6+7+8+9 = 35.
ответ: 35 грамм.
ответ: 2*x³+5*x²+x-2=(x+1)*(x+2)*(2*x-1).
Объяснение:
Запишем данный многочлен в виде 2*(x³+5/2*x²+1/2*x-1). Для того, чтобы разложить многочлен в скобках на множители, нужно решить уравнение x³+5/2*x²+1/2*x-1=0. Это - приведённое кубическое уравнение, поэтому одним из его целых корней (если они есть) может быть целый делитель свободного члена данного уравнения, то есть числа -1. Таких делителей всего два: 1 и -1. Подставляя значения x=1 и x=-1 в данное уравнение, находим, что число x=1 не является корнем уравнения, а число x=-1 - является. Теперь разделим многочлен x³+5/2*x²+1/2*x-1 на двучлен x-(-1)=x+1. После этого получим тождество x³+5/2*x²+1/2*x-1=(x+1)*(x²+3/2*x-1). Теперь разложим на множители квадратный трёхчлен x²+3/2*x-1, для чего нужно решить уравнение x²+3/2*x-1=0. Оно имеет корни x1=1/2 и x2=-2, поэтому x²+3/2*x-1=0=(x-1/2)*(x+2). Тогда x³+5/2*x²+1/2*x-1=(x+1)*(x-1/2)*(x+2) и окончательно 2*x³+5*x²+x-2=(x+1)*(x+2)*(2*x-1).
Відповідь:
Пояснення:
Из треугольника CDH
Так как сумма углов треугольника 180°, а угол СHD уже равен 90°,
То сумма двух остальных углов будет равна 180°-90°=90°.
Тогда, что бы найти неизвестный угол нужно 90° минус известный угол, который у нас 45°.
Поэтому и 90° - 45°