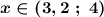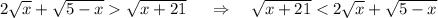
В левой части стоит квадратный корень, который неотрицателен . Значит он может быть меньше только положительного выражения . Но сумма квадр. корней тоже неотрицательна . Поэтому условие положительности суммы квадр. корней можно не писать .
ОДЗ: 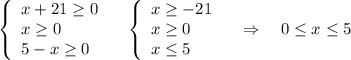
Возведём в квадрат обе части неравенства .
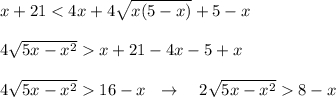
Теперь неравенство будет эквивалентно совокупности двух систем.
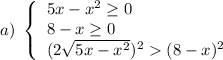 или
или 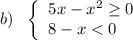
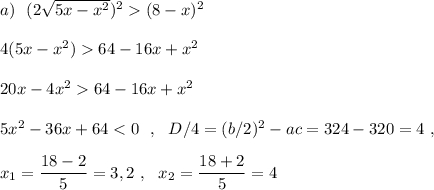
Нашли нули функции 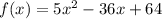 .
.
Решаем неравенство 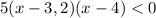 методом интервалов. Наносим нули функции на числовую ось и вычисляем знаки на получившихся промежутках . Надо выбрать любое число, принадлежащее интервалу , подставить его в функцию, и определить , какой знак принимает ф-ция в нужном интервале .
методом интервалов. Наносим нули функции на числовую ось и вычисляем знаки на получившихся промежутках . Надо выбрать любое число, принадлежащее интервалу , подставить его в функцию, и определить , какой знак принимает ф-ция в нужном интервале .
Например,
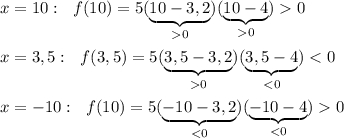
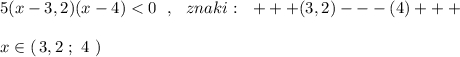
![5x-x^2\geq 0\ \ \to \ \ x(5-x)\geq 0\ \ ,\ \ x(x-5)\leq 0\ \ \Rightarrow znaki:\ \ +++[\, 0\,]--[\, 5\,]+++\ \ ,\ \ \ \ x\in [\ 0\ ;\ 5\ ]16-2x\geq 0\ \ \to 16\geq 2x\ \ ,\ \ 2x\leq 16\ \ ,\ \ x\leq 4\ \ \Rightarrow \ \ x\in (-\infty \, ;\, 4\ ]](/tpl/images/4978/1070/6c51f.png)
![\left\{\begin{array}{l}x\in (\ 3,2\ ;\ 4\ )\\x\in [\ 0\, ;\, 5\, ]\\x\in (-\infty \, ;\, 4\ ]\end{array}\right\ \ \ \Rightarrow \ \ \ \ \ \boldsymbol{x\in (\ 3,2\ ;\ 4\ )}](/tpl/images/4978/1070/7ece0.png)
![b)\ \ \left\{\begin{array}{l}5x-x^2\geq 0\\8-x < 0\end{array}\right\ \ \left\{ {\begin{array}{l}x\, (5-x)\geq 0\\x 8\end{array}\right\ \ \left\{\begin{array}{l}x\in [\ 0\, ;\, 5\, ]\\x\in [\, 8\, ;+\infty \, )\end{array}\right\ \ \Rightarrow \ \bf x\in \varnothing](/tpl/images/4978/1070/1f703.png)
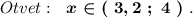
(x+1)(x^2-x+1)-x(x+3)(x-3) Упростим данное выражение, для этого раскроем скобки. Также заметим, что (x+1)(x^2-x+1) - это формула сокращенного умножения: a³+b³=(a+b)(a²-ab+b²) , где, в нашем случае, a - это x, а b - это x, таким образом, (x+1)(x^2-x+1)=x³+1.
Заметим, (x+3)(x-3) - тоже формула сокращенного умножения - разность квадратов
(x+3)(x-3)=x²-9/ Преобразуем наше выражение, дораскрываем скобки:
(x+1)(x^2-x+1)-x(x+3)(x-3)=x³+1-x(x²-9)=x³+1-x³+9x=9x+1.
Найдем значение выражение при x=1:
9*1+1=10.
Удачи!
Объяснение:
Из равенства xy = yx следует, что делители чисел x и y одни и те же, то есть То же самое равенство показывает, что a1y = b1x, ..., any = bnx. Пусть для определённости x < y. Тогда из записанных равенств следует, что a1 < b1, ..., an < bn, то есть y = kx, где k – целое число. Подставляя равенство y = kx в исходное равенство xy = yx, получаем xkx = (kx)x, то есть xk–1 = k. По предположению k > 1, а значит, x > 1. Ясно, что 22–1 = 2. Легко также проверить, что если x > 2 или k > 2, то xk–1 > k.
ответ
{2, 4}.
ответ :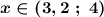
Объяснение:
ОДЗ :
Возведем в квадрат
Данный промежуток удовлетворяет ОДЗ :
ответ :