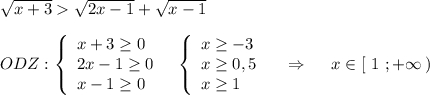
Так как правая и левая части неравенства неотрицательны, то можно его возвести в квадрат .
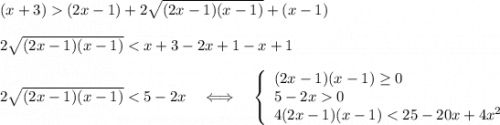
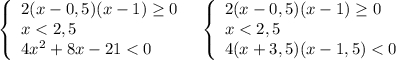
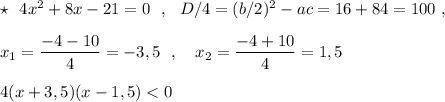
Метод интервалов решения неравенств .
Знаки функции: 
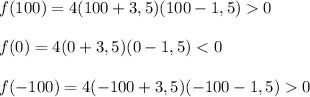
Выбираем интервал, где записан знак минус : 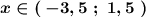 .
.
![\star \ \ 2(x-0,5)(x-1)\geq 0znaki:\ \ \ +++[\ 0,5\, ]---[\ 1\ ]+++\ \ ,\ \ \ \boldsymbol{x\in (-\infty ;\, 0,5\ ]\cup [\ 1\ ;+\infty )}\ \ \star](/tpl/images/4978/1100/dee8b.png)
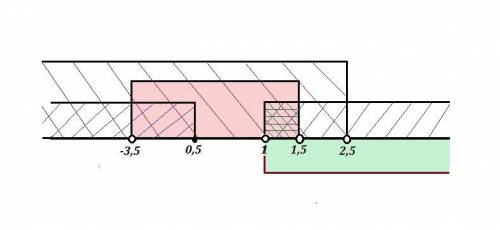
![a)\ \ \left\{\begin{array}{l}x\in (\, -3,5\ ;\ 1,5\ )\\x < 2,5\\x\in (-\infty ;\, 0,5\ ]\cup [\ 1\ ;+\infty )\end{array}\right\ \ \ \ \Rightarrow \ \ \ \ \boldsymbol{x\in (-3,5\ ;\ 0,5\ ]\cup (\ 1\ ;\ 1,5\ )}b)\ \ \left\{\begin{array}{l}x\in (-3,5\ ;\ 0,5\ ]\cup (\ 1\ ;\ 1,5\ )\\x\in [\ 1\ ;+\infty \, )\end{array}\right\ \ \ \ \ \Rightarrow \ \ \ \boldsymbol{x\in (\ 1\ ;\ 1,5\ )}Otvet:\ \ \boldsymbol{x\in (\ 1\ ;\ 1,5\ )}\ .](/tpl/images/4978/1100/e57d7.png)
1)
1/7*(0,14+2,1-3,5) =
= 1/7 * (14/100 + 21/10 - 35/10) =
= 1/7 * 14/100 + 1/7 * 21/10 - 1/7 * 35/10 =
= 1/50 + 3/10 - 5/10 = 1/50 + 15/50 - 25/50 = -9/50 (или -0,18),
2)
1/12*(4,8-0,24-1,2) =
= 1/12*(48/10 - 24/100 - 12/10) =
= 1/12 * 48/10 - 1/12 * 24/100 - 1/12 * 12/10 =
= 4/10 - 1/50 - 1/10 = 20/50 - 1/50 - 5/50 = 14/50 = 7/25 (или 0,28),
3)
(18 6/7 + 21 3/4) : 3 =
= ((18 + 21) + (6/7 + 3/4)) : 3 =
= (39 + (24/28 + 21/28)) : 3 =
= (39 + 45/28) : 3 = 39 : 3 + 45/28 : 3 =
= 13 + 45/28 * 1/3 = 13 + 15/28 = 13 15/28,
4)
(15 5/7 + 20 15/16 ) * 1/5 =
= ((15 + 20) + (5/7 + 15/16)) * 1/5 =
= (35 + (80/112 + 105/112)) * 1/5 =
= (35 + 185/112) * 1/5 = 35 * 1/5 + 185/112 * 1/5 =
= 7 + 37/112 = 7 37/112
1)
1/7*(0,14+2,1-3,5) =
= 1/7 * (14/100 + 21/10 - 35/10) =
= 1/7 * 14/100 + 1/7 * 21/10 - 1/7 * 35/10 =
= 1/50 + 3/10 - 5/10 = 1/50 + 15/50 - 25/50 = -9/50 (или -0,18),
2)
1/12*(4,8-0,24-1,2) =
= 1/12*(48/10 - 24/100 - 12/10) =
= 1/12 * 48/10 - 1/12 * 24/100 - 1/12 * 12/10 =
= 4/10 - 1/50 - 1/10 = 20/50 - 1/50 - 5/50 = 14/50 = 7/25 (или 0,28),
3)
(18 6/7 + 21 3/4) : 3 =
= ((18 + 21) + (6/7 + 3/4)) : 3 =
= (39 + (24/28 + 21/28)) : 3 =
= (39 + 45/28) : 3 = 39 : 3 + 45/28 : 3 =
= 13 + 45/28 * 1/3 = 13 + 15/28 = 13 15/28,
4)
(15 5/7 + 20 15/16 ) * 1/5 =
= ((15 + 20) + (5/7 + 15/16)) * 1/5 =
= (35 + (80/112 + 105/112)) * 1/5 =
= (35 + 185/112) * 1/5 = 35 * 1/5 + 185/112 * 1/5 =
= 7 + 37/112 = 7 37/112
√(х+3) >√(2х-1)+ √(х-1).
2)D(f)
{x+3≥ 0,
{2x-1≥ 0,
{x-1≥0. Общее решение данной системы x≥ 1.
1) Возводим обе части в квадрат , тк левая и правые части положительны
х+3>2х-1+2√(2х-1)*√(х-1)+х-1,
5-2х>2√(2х²-3х+1). После возведения в квадрат получаем
25-20х+4 х²> 8х²-12х+4,
4х² +8х-21<0.
3)Нули функции f=4х² +8х-21.
4х² +8х-21=0 ,D=400, x1=1,5 , x2=-3,5.
Тогда 4(х-1,5)(х+3,5)<0
4)Найдем знаки функции на [1;+беск).
Значение -3,5∉[1;+беск).
4(х-1,5)(х+3,5)<0
[1] - - - - [1,5]+ + +
Определим знак последнего интервала f(2)=4*2²+8*2-21=11>0. На этом интервале ставим знак «+».
5) ответ. [1;1,5]