Составляем систему, чтобы выразить q (знаменатель геом.пр.) :
Решаем:
делим первое уравнение системы на второе, получаем:
[2]
Составим и решим систему, чтобы получить значения и :
Получаем корни:
или
Находим :
Так как , то:
или
Заметим: что в , что в - выходят одинаковые значения (36 и 9). От перестановки слагаемых сумма не меняется. Поскольку у нас возрастающая прогрессия, возьмем за , а за
Чтобы найти первый член прогрессии, находим ещё и :
Формула:
Решение:
И теперь мы можем с формулы n-ого члена геометрической прогрессии: , вывести первый член прогрессии. Значит:
Допустим, автобус выходит из А в 6 утра и приходит в В в 10. Следующий выходит в 7, потом в 8, в 9, в 10, в 11, в 12, в 13. Придя в 10 утра в В, он разворачивается и едет обратно. В А он возвращается в 14. Автобус, который вышел из А в 7, к 10 часам проедет 3/4 дороги. А в 10:30 он проедет 3/4 + 1/8 = 7/8 и встретит первый автобус, который в 10 вышел из В. Автобус, который вышел в 8, к 10 часам проедет 1/2 дороги. А в 10:30 он проедет 1/2 + 1/8 = 5/8 дороги. И ровно в 11 он проедет 3/4 дороги и встретит первый автобус. И дальше все точно также. Таким образом, если я увидел встречный автобус, то следующий я увижу через полчаса.
[1]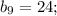
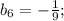
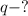
Формула n-ого члена геометрической прогрессии: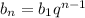
Распишем для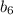 и
и 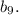
Составляем систему, чтобы выразить q (знаменатель геом.пр.) :
Решаем:
[2]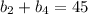
Составим и решим систему, чтобы получить значения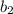 и
и 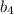 :
:
Получаем корни:
Находим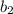 :
:
Так как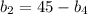 , то:
, то:
Заметим: что в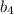 , что в
, что в 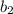 - выходят одинаковые значения (36 и 9). От перестановки слагаемых сумма не меняется. Поскольку у нас возрастающая прогрессия, возьмем за
- выходят одинаковые значения (36 и 9). От перестановки слагаемых сумма не меняется. Поскольку у нас возрастающая прогрессия, возьмем за 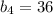 , а за
, а за 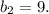
Чтобы найти первый член прогрессии, находим ещё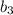 и
и 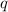 :
:
Формула: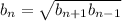
Решение: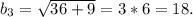
И теперь мы можем с формулы n-ого члена геометрической прогрессии: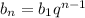 , вывести первый член прогрессии. Значит:
, вывести первый член прогрессии. Значит: